Brian Trial

Brian has loved recreational mathematics since the late 70's when he discovered Martin Gardner's books in his middle school library, and has loved computers since his first one, a Texas Instruments TI-99/4A bought on clearance.

In 2007 Brian developed a program for creating solutions to the 1xn perfect squared rectangle problem. In 1960 Victor Klee included in his problem survey of Unsolved Intuitive Problems in Geometry p34-36 Problem K12 Squaring the rectangle, the "PROBLEM: What numbers can be attained as the ratio of the two dimensions of a simply perfectly squared rectangle? In particular, can the number 2 be so attained?"[3]. Solutions for the number 2 (a 1x2 simple perfect squared rectangle) were found by Federico[1] and Duijvestijn[2] and for 3 by Skinner, with a 1x3 solution. Brian found solutions to numbers 4 to 18 with 1x4(2), 1x5(2), 1x6, 1x7, 1x8, 1x9, 1x10, 1x11(2), 1x12, 1x13, 1x14, 1x15, 1x16, 1x17 and 1x18 simple perfect squared rectangles. See here (portrait) and here (landscape). These rectangles can be fitted togther to create CPSSs. The simplest constructions being 2 (scaled) rectangles and a large additional square. For an example of a CPSS constructed from a 1x17 & 1x18 the largest element square is 17/18 (approximately 94%) of the CPSS side. The smaller elements are dwarfed by the larger square, you need to zoom in to see them along the sides. The order is 560 and the size is 33,821,736.

Simple Perfect Squared Rectangles of Lowest Order in Ratios 2:1 and 3:1

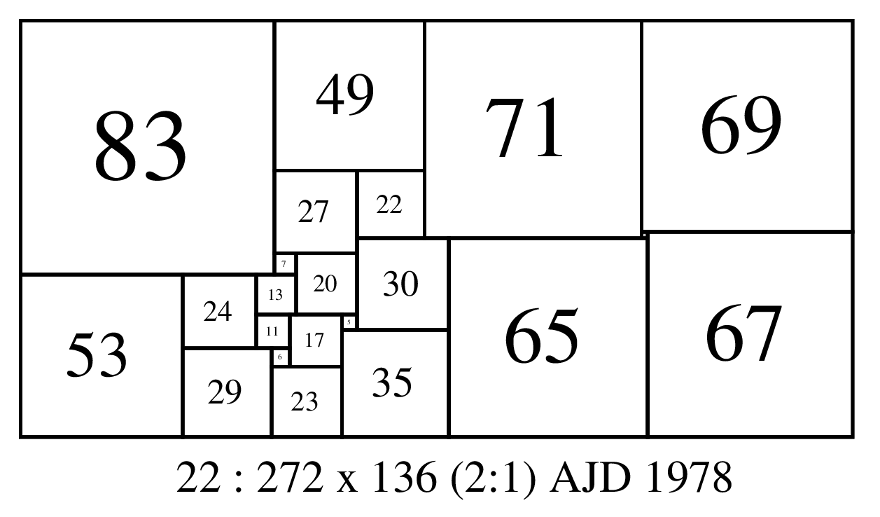
P.J. Federico gave examples of several simple perfect 2 x 1 squared rectangles [1]. The 2 x 1 simple perfect squared rectangle of lowest order (order 22) was found by Duijvestijn [2] in 1978. "On September 2nd, 1978 a lowest-order simple perfect 2x1 squared rectangle was found. Its Bouwkamp code reads as follows: (83,49,71,69)(27,22)(2,67)(30,65)(7,20)(53,24,13)(11,17, 5)(35)(29,6)(23). It is shown in Figure 1. All 3-connected planar graphs (so-called c-nets) of orders 6 up to and including 22 are available on magnetic tape and magnetic disk. The order of a c-net is the number of its edges. These c-nets were used to fmd the lowest- order simple perfect squared square. The c-nets were also used to search for the existence of solutions of 2 x 1 squared rectangles. It appears that there do not exist simple perfect 2 x 1 squared rectangles of orders lower than 22. The order of a squared rectangle is the number of its elements (squares). Below order 22 there only exist imperfect 2 x 1 squared rectangles. The number of simple imperfect 2 x 1 squared rectangle solutions is, however, small compared with the number of simple imperfect squared square solutions." [2]

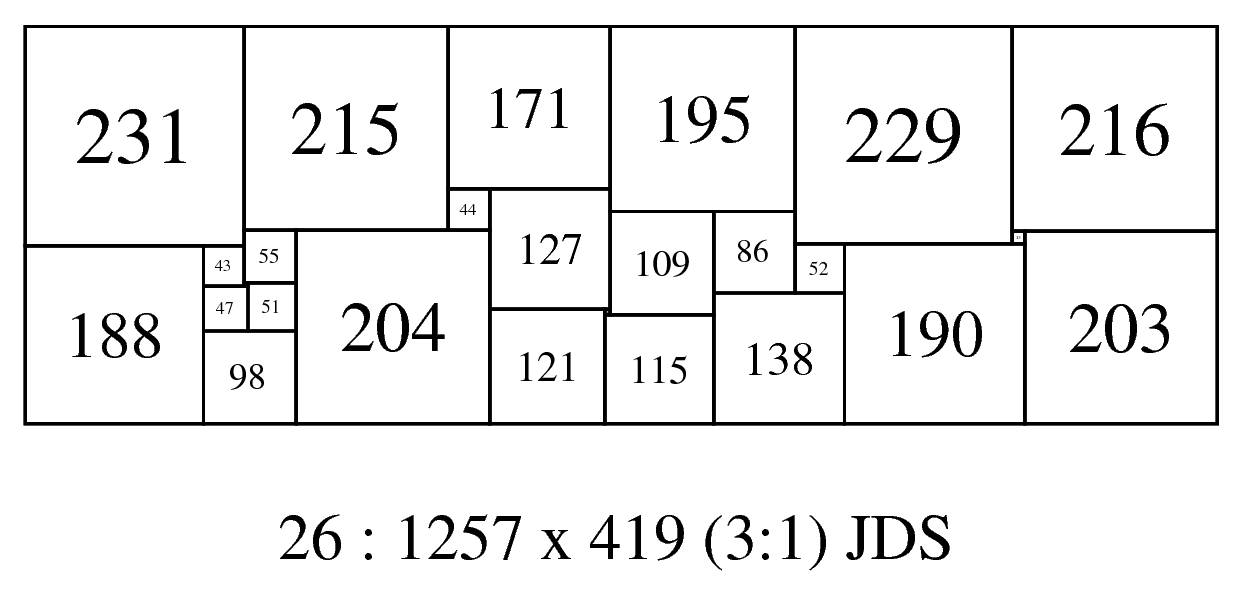
In the late 1990s, Jasper Dale Skinner searched all simple perfect squared rectangles up to order 26 to find a 3x1 rectangle. He found the lowest order (order 26) simple perfect squared rectangle with dimensions of 1257 x 419 in this ratio. It's Bouwkamp code is; (231,215,171,195,229,216)(44,127)(109,86)(55,204)(13,203)(52,190)(188,43)(4,51)(47)(138)(121,6)(115)(98)

Simple Perfect Squared Rectangles, by Brian Trial, Ferndale, Michigan, USA

4x1(2), 5x1(2), 6x1, 7x1, 8x1, 9x1, 10x1, 11x1(2), 12x1, 13x1, 14x1, 15x1, 16x1, 17x1 and 18x1 Simple Perfect Squared Rectangles.

Images and Bouwkamp codes for Brian Trial's simple perfect squared rectangles in the ratio nx1, including examples of all ratios from 4x1 up to 18x1.

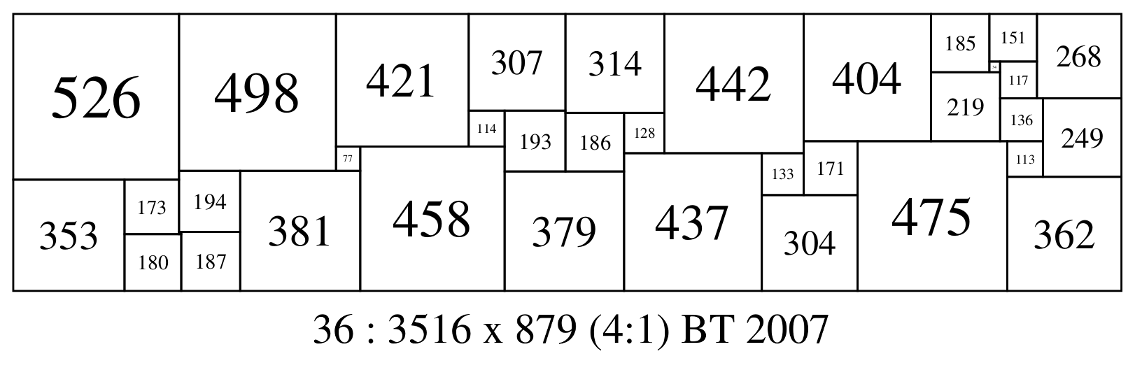
36 3516 879 (526,498,421,307,314,442,404,185,151,268) (34,117) (219) (136,249) (114,193) (186,128) (171,475,113) (77,458) (437,133) (194,381) (379) (362) (353,173) (304) (7,187) (180) * 36 : 3516 x 879 (4:1) BT 2007

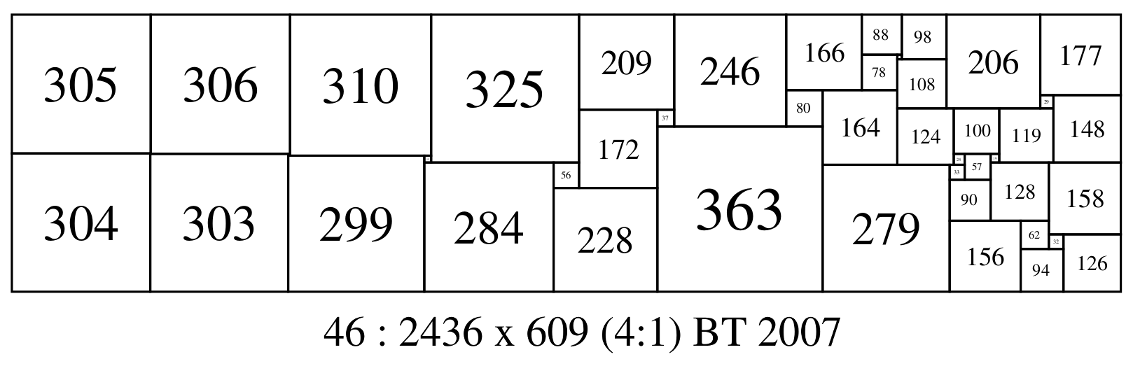
46 2436 609 (305,306,310,325,209,246,166,88,98,206,177) (78,10) (108) (80,164) (29,148) (124,100,119) (172,37) (363) (304,1) (303,4) (24,57,19) (299,15) (284,56) (128,158) (279,33) (90) (228) (156,62) (32,126) (94) * 46 : 2436 x 609 (4:1) BT 2007

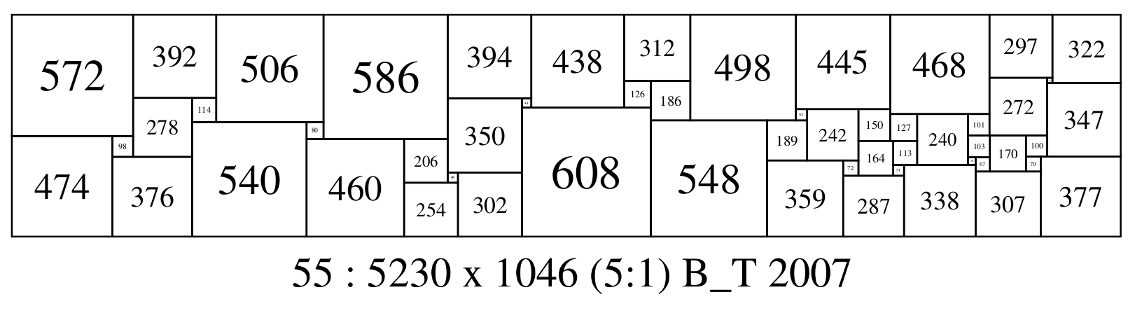
55 5230 1046 (572,392,506,586,394,438,312,498,445,468,297,322) (272,25) (126,186) (347) (278,114) (350,44) (608) (53,242,150) (127,240,101) (548,189) (540,80) (103,170,100) (474,98) (460,206) (164,113) (70,377) (376) (36,67) (359,72) (51,338) (307) (48,302) (287) (254) * 55 : 5230 x 1046 (5:1) B_T 2007

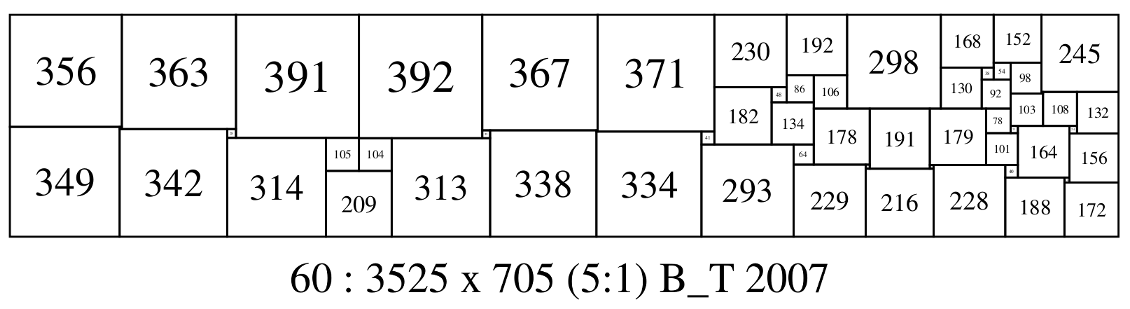
60 3525 705 (356,363,391,392,367,371,230,192,298,168,152,245) (54,98) (130,38) (86,106) (92) (182,48) (5,108,132) (103) (134) (178,191,179,78) (23,164,24) (349,7) (342,28) (25,338,4) (334,41) (101) (156) (314,105) (104,313) (293,64) (229,13) (12,228,40) (216) (209) (188,16) (172) * 60 : 3525 x 705 (5:1) B_T 2007

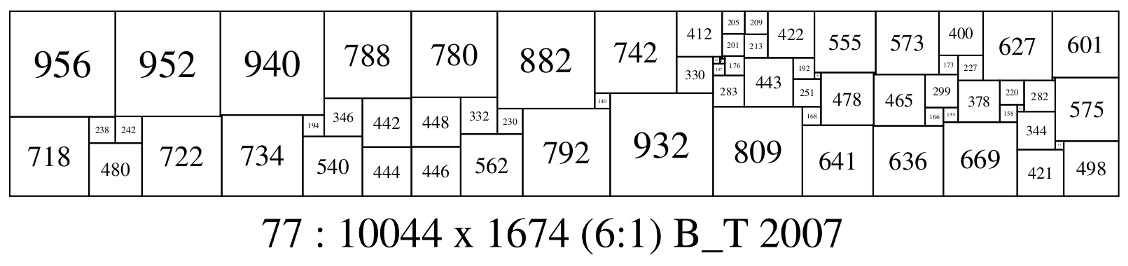
77 10044 1674 (956,952,940,788,780,882,742,412,205,209,422,555,573,400,627,601) (201,4) (213) (173,227) (25,176) (330,63,19) (443,192) (44) (107) (59,478,18) (465,299) (283) (26,575) (251) (378,220,282) (140,932) (448,332) (346,442) (158,62) (809,168) (166,133) (230,792) (344) (12,734,194) (242,722) (718,238) (669) (641,5) (636) (562) (540) (77,498) (480) (2,446) (444) (421) * 77 : 10044 x 1674 (6:1) B_T 2007

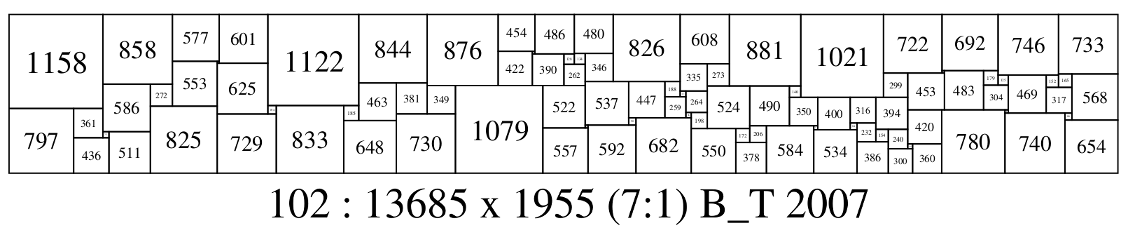
102 13685 1955 (1158,858,577,601,1122,844,876,454,486,480,826,608,881,1021,722,692,746,733) (422,32) (134,346) (390,128) (553,24) (625) (335,273) (262) (30,483,179) (299,453) (165,568) (125,469,152) (537,447,188) (463,381) (586,272) (304) (349,1079,522) (524,490,140) (317) (71,264) (259) (350,400,316,394) (104,833,185) (825) (797,361) (420,780,40) (66,198) (740,86) (730) (729) (90,682) (654) (648) (84,232) (35,592) (206,584,50) (557) (550,172) (154,240) (534) (75,511) (436) (386) (378) (60,360) (300) * 102 : 13685 x 1955 (7:1) B_T 2007

142 14656 1832 (941,991,750,589,431,585,305,330,685,501,818,542,615,553,421,710,755,465,640,911,730,756,632) (280,25) (355) (132,289) (277,154) (290,175) (184,317) (318,224) (62,623) (557,462) (470,119) (151,526) (189,443) (544,271) (362,306,556) (396) (466,488,45) (181,523,26) (441,309) (661,429) (458,259,65) (375) (477,256,291,111) (254) (69,249) (273,360,405,325) (180) (891,50) (841,200) (56,250) (199,60) (95,785) (388,391) (221,35) (757) (358,38) (723,32) (691,242) (690) (207,656,226) (353,648,245) (641) (204,284) (39,618) (308,17) (591,215) (579) (158,202) (161,537) (157,248) (449) (430) (66,416,179) (403) (385,3) (382,12) (376) (370) (359) (350) (58,295) (20,288) (268) (237) * 142 : 14656 x 1832 (8:1) B_T 2007

111 14679 1631 (919,828,555,837,1018,654,774,811,839,914,523,592,730,417,521,389,646,498,460,479,449,340,486) (109,231) (132,257) (313,104) (147,411) (38,403,19) (381,117) (85,401) (171,365) (342,415) (454,69) (273,282) (316) (502,159) (264) (290,373,217,23) (534,120) (194) (21,201,419,402) (180) (857,37) (820,28) (298,803) (794,325) (792,75) (258,771,27) (269,73) (156,768,255) (744) (717,272) (712,207) (163,218) (695,83) (209,245) (144,613,261) (612) (128,537) (513) (505) (172,499) (482,155) (469) (445,36) (91,443) (409) (352) (327) * 111 : 14679 x 1631 (9:1) B_T 2007

169 21280 2128 (1074,1094,1174,1120,731,537,328,447,371,666,758,665,584,595,785,605,492,623,799,849,773,684,449,663,384,399,607,838,810,628,748) (209,119) (76,295) (369,15) (414) (642) (235,214) (361,131) (194,552) (155,418,11) (407,199) (357,248) (206,401) (578,176) (351,277) (787,90) (93,498,74) (400,469,92) (89,830) (389,536) (229) (157,591) (459) (538,405) (204,658) (9,217,375,184) (208) (402,523,50) (28,613,169) (620) (170,696) (311,460,128) (261,348) (434) (7,198,152) (195,34) (191) (332) (241,279) (1126,158) (571) (23,377) (1054,20) (178,1039) (1034,80) (46,367) (354,1008,147) (308,161) (968) (162,149) (133,965) (954,300) (280,927,121) (238,221) (203,38) (317) (861) (832) (819,122) (806) (236,789) (111,705) (697,83) (695,146) (685) (347,678) (654) (647) (614,299) (213,594) (553) (549,168) (381) (16,331) (315) * 169 : 21280 x 2128 (10:1) B_T 2007

158 32285 2935 (1652,1476,948,1368,1589,1635,1552,1638,1524,898,594,612,1037,793,1072,982,834,777,883,758,1256,1365,1509,1582,1104,944,946,957) (576,18) (630) (260,498) (57,614,106) (244,549) (334,557) (508,346,135) (626,272) (160,782,2) (937,11) (528,420) (968) (90,706,186) (395) (205,1076) (270,892) (478,786) (520) (848) (162,184) (835) (736,909,109) (819) (740,590,144) (1567,221) (297,1544) (579) (545,1459) (446,352,610,245) (541,639,604,366) (83,1383,86) (172,589,707,592) (1346,464) (418,1300) (1297,427) (1283,369) (276,1247) (625,157) (417) (94,258) (1052,42) (238,128) (284,502) (1010) (150,980) (197,971) (943,372) (917,59) (914) (882) (870,98) (858,36) (60,830) (822,290) (816,52) (35,807) (242,774) (772) (199,770) (764,294) (115,761) (176,646) (41,584) (571) (543) (532) (470) * 158 : 32285 x 2935 (11:1) B_T 2009

168 34276 3116 (1867,1815,1672,1757,1847,1133,1367,979,630,569,796,913,1037,1036,943,752,574,845,681,1184,895,1142,985,886,1012,634,890,1229, 1099,1288,812,1007) (342,227) (178,396) (349,281) (378,256) (164,517) (191,739) (738,285) (617,195) (125,884) (99,661,126) (807,339) (648,247) (623) (168,621,124) (93,493,548) (521) (240,332,756) (157,927) (1202) (831,685) (291,838) (871,290) (453) (130,780,189) (899,234) (688,858) (14,811,359) (531) (148,92) (395,717,586) (591,334,411,141) (424) (581) (1749) (758) (438,55) (1625,238) (201,1582,652) (452,555) (365,296) (257,77) (73,322) (143,1444,85) (146,1419) (488) (1387,266) (1381) (1359,483) (657,1301) (131,455) (518,170) (1273) (393,1269,185) (1249,618) (34,1242) (391,1237) (278,1208) (88,1204) (1170) (1121,408) (1116) (1084) (305,250) (930) (929,317) (295,907) (876) (846) (768) (713) (13,644) (631) (612) * 168 : 34276 x 3116 (11:1) B_T 2009

174 25644 2137 (1280,1236,1115,1087,1096,1160,924,1034,634,472,764,779,781,688,582,1058,1104,721,1021,572,738,618,625,773,742,506,604,609,531, 984,806) (180,292) (408,98) (78,453) (406,166) (106,476) (697,5) (692) (120,491,7) (484,148) (400,216,18) (198) (93,701) (421,300) (314,339,371) (31,539,172) (500,541,15) (322,630) (526,268) (266,608) (178,628) (414) (580) (483,441) (43,363) (527,638,450) (548,496,320) (331,1103) (534) (289,25) (494,566,428,46) (364) (28,1050,9) (14,308) (1041,64) (382,278,452,38) (332,1028) (121,1022) (459) (977,247) (456,901) (873,41) (857,423) (326,213) (343,836,210) (832,276) (176,796) (772) (104,174) (398,748,163) (734,204) (730) (375,703) (696) (263,651) (643,150) (626,111) (52,620) (585,72) (581,45) (32,568) (556,254) (536) (530) (515,234) (513,125) (493) (11,445) (434) (388) (48,350) (47,328) (302) (281) * 174 : 25644 x 2137 (12:1) B_T 2007

186 44837 3449 (1908,1468,1470,1924,1966,2058,1369,1815,2062,1560,853,599,944,1221,1719,1261,921,1336,1243,967,1383,1198,1350,684,702,1422,1329, 1423,1135,1140,1448,832,995,1132) (254,345) (666,18) (720) (669,163) (1107) (448,473) (1012,277) (551,416) (1021,137) (1269) (288,842,5) (837,308) (185,861,152) (1000,498) (93,875,275) (489,664,108) (332,903,94) (58,589,782) (709,542,917) (923,446) (556) (961,1023) (531) (955,948,239) (928,877) (413,710,426,207) (807,661) (659,811) (154,515) (826) (797,763) (361) (571) (502,891,793,31) (520) (1634,627) (116,297) (284,142) (167,375) (1541,367) (357,1525,42) (623,1524,193) (747,265) (363,744) (1483,525) (323,1472) (1433,606) (433,1391,234) (347,1390) (380,1387,295) (1331,519) (1320) (1291) (1228,539) (138,1217,119) (1182,110) (242,278) (1174) (1168) (1157) (51,1149) (1126) (293,1105,389) (1098) (1092) (7,1079) (1072) (221,1048) (327,1043) (1007) (958) (98,937) (901) (150,839) (827) (812) (1,746) (745) (716) (689) * 186 : 44837 x 3449 (13:1) B_T 2009

252 50036 3574 (1826,1904,1170,851,621,1012,631,881,731,1049,1158,1545,1413,1755,1516,1195,1184,1461,903,1174,1059,1491,993,593,786,663, 1203,1350,992,1520,1662,1342,1507,1451,1018,1230,1464,1029,1466,769,841,617,1010) (400,193) (224,393) (230,391) (381,250) (123,540) (413,318) (697,72) (1102) (1137) (319,762) (868,263) (632,271) (464,528) (498,895) (1403) (601,446,737) (806,212) (592,437) (1258,109) (493,566) (676) (880,387) (1046,443) (1067,378) (11,896,277) (321,885) (685,911,147) (1023,419) (320,857,165) (764,627,106) (295,753,365) (364,714,373) (570) (155,291) (626,1038,74) (185,1122,157) (904,724,972) (134,834,1021) (692,658,322) (239,754,844) (815,1091,142) (706) (790,979,163) (871) (1961) (749) (700) (604) (848,531,745) (458) (1825,71) (23,411,655,390,515) (388) (14,350) (747) (777,402) (1748,78) (336) (770,1686,226) (1670,312) (578,49) (460,677) (619) (269,611) (280,1494,7) (633) (1460,441) (265,125) (34,1409,615) (358,1408,244) (180,544) (317,214) (208,1375) (1358) (375,27) (258,1333,182) (1321,333) (1304,90) (260,1267) (98,1249,187) (314,476) (310,505) (1214) (629,1204) (1167) (1164) (242,1161) (1151) (296,1136) (221,1075) (101,1064) (1062,146) (287,1050) (1019) (1007) (988,467) (179,973) (229,963) (929) (925) (919) (916) (854) (840) (794) (763) (734) (54,575) (521) * 252 : 50036 x 3574 (14:1) B_T 2009

211 49605 3307 (1975,1791,1285,1600,1029,1487,1612,1654,1697,1827,1778,1501,919,1256,747,425,528,1031,1066,1334,819,756,1145,1472,1476, 1094,948,683,696,1189,1171,980,957,1056,1261,1129,1169,1666,1478,849,1069) (322,103) (631) (670,13) (709) (509,560) (367,389) (515,304) (629,220) (582,337) (543,405) (23,835,99) (191,812) (571,458) (128,868,35) (950,205) (833,268) (1289) (697,397) (671) (374,715,40) (649,558,327) (759) (663,546) (18,723,621) (216,991) (2051,51) (608,583,275) (506,779) (611) (839,818,460) (1075) (925) (698,726,371,4) (383,782,315) (401,755,951) (1820,125) (940) (277,1806) (33,341) (308) (464,1707) (1695,42) (1653,43) (49,644,713,260) (1610,130) (91,467) (595) (526,1529) (781,1516) (599,413) (539,1515,214) (358,1513) (1480,477) (12,651) (355,16) (496,1463) (399) (137,471) (47,354) (286,437) (19,1408,274) (1389) (307) (1332,643) (1301) (1243) (21,1155) (1137,28) (1134) (150,1127) (1109) (186,227) (146,1074,196) (1049,132) (1003) (173,997,69) (98,977) (976) (967) (340,949) (928) (917) (294,879) (878,269) (876,291) (824) (46,735) (689) (609) (585) * 211 : 49605 x 3307 (15:1) B_T 2009

295 65472 4092 (2066,1342,1232,1345,687,716,1461,1797,1245,1247,1791,1228,1237,796,1151,1209,1322,1356,1283,1203,1150,1018,762,882,1378, 1521,1416,921,855,715,868,1055,1001,900,1186,845,1349,1336,1631,1056,1537,1147,843,1178,1205,1117,769,1190,1223,1382,1982,1943,1085,1312) (658,29) (562,153) (745) (256,506) (348,421) (441,355) (304,539) (341,504) (433,422) (719,302) (386,496) (101,799) (554,367) (54,1048) (132,1142) (115,994) (575,481) (858,227) (88,848,529) (390,1061) (53,1229) (1448,58) (417) (204,947,27) (513,1014) (456,1122,33) (80,1176) (560,760) (922,345) (1097,159) (679,549) (110,1009,113) (540,1138) (552,693) (648,599) (892) (984) (73,1290) (800) (1539) (232,809,281) (13,1028,295) (553,899) (896,1220) (851,1015) (247,1182) (782,949,143) (743) (938,603) (105,580,672,59) (1121,749,336) (613) (806,963) (1135,602,671) (577) (674,462) (528) (1212,1289) (319,666) (811,501) (360,200) (1089) (55,709,911,116) (790,452,566,877) (654) (171,382) (43,605) (795) (736) (39,854,870,477,561) (2127) (3,609,594,815) (606) (488,92) (2043,461) (2026,211) (2004,173) (83,1967) (468,1961,407) (533,69) (717,1932,167) (310,1892,164) (1884) (372,377) (629,1851,324) (338,114) (1831) (593) (1780,8) (1772,271) (1765,157) (680) (1728,479) (491,647) (194,1713,498) (393,84) (1608) (174,1592,202) (645) (1582) (1554,35) (1527,17) (1519) (15,579) (1510) (1505) (1501) (423,1493) (248,1420) (369,1418) (1390,518) (358,1295,16) (1279) (1249,442) (298,1241) (354,1226) (1222) (1215) (365,1172) (1070) (1049) (943) (937) (872) (807) * 295 : 65472 x 4092 (16:1) BT 2009

270 79169 4657 (2350,2393,2565,2408,1765,2239,1412,1997,1919,1022,1147,1453,1940,1650,2723,1471,1304,1422,1080,1269,789,1098,1134,1222,1492, 1028,1394,1142,1035,785,962,1566,1256,1910,1169,919,1160,1322,1729,1571,1038,1528,1585,1177,1120,1626,927,1155,891,1145,886,1068,1270,938,1164,1439) (250,535) (480,309) (704,182) (637,254) (678,241) (699,228) (712,226) (358,604) (897,125) (464,564) (107,1178) (548,490) (1048,202) (342,738) (1371,36) (614,506) (1082,88) (488,761) (954,445) (1272) (944,439) (1239,162) (1115,275) (741,428) (620,557) (1040,270) (602,654) (549,1200) (1009,463) (666,638) (893) (1077,407) (198,960,236) (827,585) (520,1244) (1714) (966,487) (972,499) (770,1456) (736,896,386) (66,571) (647,1231,292) (530,1026,15) (329,1044,212) (563) (509,640) (762) (505) (1106) (1564,1267) (724) (290,1360) (83,629) (670,1094,372) (546) (1171) (643,1122) (832) (1287) (894) (451,310) (842,628,1042,793) (715) (78,2738) (2717) (1158) (1165) (2660) (794,2558,131) (406,496) (885,163) (448,115) (2444,584) (253,829) (771) (648,2418) (783,1027) (851) (2378,1084) (2307,43) (594,2303) (2264,172) (304,2258,424) (802,2249) (2238) (691,205) (280,692) (636,2188) (316,90) (214,414) (2092,645) (2060) (2028,768) (434,810) (249,1954) (287,1934,782) (45,1905) (1860) (1834) (1770) (297,1764) (492,679) (341,1709) (1705) (1656) (1647) (1612) (35,1557) (371,1552) (1542) (370,1522) (210,1504) (394,1467) (1447) (1368) (1294) (1260) (1181) (1152) (1073) * 270 : 79169 x 4657 (17:1) BT 2009

289 72648 4036 (2040,2084,2260,2464,2200,1864,1220,1796,1928,1880,1888,1236,1496,1221,1289,1010,1493,1353,1632,958,1242,1396,1578,1168,866, 1411,1575,820,885,1480,1211,734,991,831,1276,1204,691,869,1017,777,1314,1340,760,940,881,1703,1020,1357,1769,1938,1901,1073,1318) (513,178) (477,257) (580,180) (240,537) (755,65) (160,671) (302,564) (899,148) (59,822) (950) (1179) (674,284) (1408) (279,731) (1405) (683,337) (828,245) (625,845) (325,903,489) (269,1419) (644,576) (275,878,68) (749,487) (1372,154) (226,797,253) (810,826) (579,629,643) (1563) (617,1303) (140,872,341) (1282,412) (1117,433) (19,1003,389) (583) (355,1394) (248,653,732) (227,941,603) (897) (578) (225,839,1266) (251,1112,215) (62,465,746,1033) (414,75) (403) (1071,1201,936) (714) (979) (974) (1141,871,169) (840) (2240,132) (614) (684) (1305) (336,2172) (48,995,829,8) (821,978,97) (529,50) (37,970,673,1049) (2108) (1109,1035) (679) (665,595) (846) (620,808) (1996,44) (763,34) (1952,176) (128,740) (338,1937,16) (1929) (842) (524,655) (574,79) (700,1836) (1811) (1776,660) (459,287) (231,1637,437) (407,1622,427) (320,1614) (394,1599) (456,1572,436) (101,1523,177) (70,525) (297,376) (51,1422) (1414) (244,1406) (57,1403) (265,1397,556) (270,601) (434,1393) (1371) (1346) (166,1327,157) (237,1316) (1294) (1262,464) (1215) (35,1205) (1200) (1199) (1195,498) (1170) (102,1165) (476,1162) (1161) (408,1155) (1136) (334,1132) (285,1126) (1116) (1086,339) (1079) (74,1063) (194,989) (959) (199,896,210) (841) (798) (795) (747) (697) (686) * 289 : 72648 x 4036 (18:1) BT 2009

Small elements in the corners and sides of perfect squared rectangles

Brian also has found solutions to the problem of constructing perfect squared rectangles with small elements in the corners and sides of the dissection. A square of size 5 is the smallest square possible on the boundary of a perfect squared square, a result due to Gambini, the only known examples are SPSSs in order 44 and 58, both found by Gambini. In 2010 the smallest size square known on the boundary of an SPSR was an 101x91 rectangle of order 17, and an SPSR 166x143 order 22, both with a size 6. In September 2011 Brian Trial found 3 SPSRs of order 28 with '5 on the side'. The dimensions of the 3 SPSRs are; 658x506, 749x611 and 1226x979. A pdf with all 3 tilings is here.

Simple perfect squared rectangles (SPSRs) with corner sizes of 15 and above exist in abundance, but corners of 9 and 14 appear in only 1 SPSR; order 9 33x32. No SPSRs with corner sizes 10,11,12 or 13 were known, and all orders up to order 24 have been searched. On November 2011, Brian Trial found an order 51 SPSR with 11 in the corner! No size 10, 12 or 13 has been found in a corner in any SPSR. Are these 3 sizes impossible for SPSR corners?

Munching Ells and the Trial Collection

Brian has developed "munching ells' method by “ell,” we mean any six-sided figure whose sides are parallel to the coordinate axes (Henle).

There are 4 different types of Ell depending on what quadrant the cut out section is located, which could have any rectangular shape, some quite stretched in one direction as we can see in the solutions so far. Another "munch" can be done along any one of the 6 sides of the Ell depending on the sides' relative sizes. He uses flags and the precedence order N>W>S>E>CH>CV to try to eliminate duplicate searches."

With "munching ells" Brian was able to find 114,712 SPSSs in orders where there are large gaps in the current catalogues. Brian's lowest order find is of order 34 and the highest is order 236, with the majority of finds in the orders 30s to 70s.

In 2018 Bernard Moss used a transform technique to derive thousands more SPSSs from Brian's discoveries.

REFERENCES

J. FEDERICO, Some simple perfect 2 x 1 rectangles, J. Combinatorial Theory 2 (1970), 244-296.
A. J. W. DUIJVESTIJN, A Lowest Order Simple Perfect 2 x 1 Squared Rectangle, J. Combinatorial Theory B 26, (1979), 372-374
Victor Klee Unsolved Problems In Intuitive Geometry, University of Washington, Seattle, WA 1960 with notes by Grünbaum 2010 p34-36 Problem K12.