Adrianus Johannes Wilhelmus Duijvestijn (AJWD) (1927-1998)

Known colloquially as "Arie", he was born in the Hague, the Netherlands, December 10, 1927. He earned the degree of MSC in Electrical Engineering at Technological University Delft in 1950. In 1955, earned another MSC degree, this in Mathematics at University Amsterdam. In 1962 he earned the degree of Ph. D. at Technological University Eindhoven, under the supervision of Prof. Dr. C. J. Bouwkamp, his thesis advisor.
The subject of the dissertation was "Electronic computation of squared rectangles"[4].
He worked at the Mathematical Centre at Amsterdam in the Computation Department under the direction of Prof. Dr.A van Wijngaarden from January - March 1951. From March 1951 through March 1953, he served as a naval officer. After his naval service, AJWD returned to the Mathematical Centre at Amsterdam remaining there until May 1956. In May 1956, he joined Philips Research Laboratories at Eindhoven, The Netherlands. From November 1957 to May 1958, AJWD worked in the United States of America as a resident visitor at IBM (Poughkeepsie) and at IBM Federal Systems (Gaitherbourg). He then joined Philips Computer Industries at Apeldorn, the Netherlands in 1963. AJWD became full professor of Computing Sciences, University Twente at Enschede, The Netherlands in 1965, working in this capacity through August 1989, becoming Emeritus Professor in September 1989.
AJWD served as President of the Dutch Computer Society from 1977-1981. In 1953 he married F.G. Bolck. The couple have four children: Lydia, Marieke, Ko and Guus.
Duijvestijn's 1962 thesis was titled the "Electronic computation of squared rectangles" but it was also a search for simple perfect squared squares. Using WTT's Wheel Theorem (communicated by Tutte to CJ Bouwkamp before it was published in 1961), and a WTT reduction formula for squares, Duijvestijn and Bouwkamp were able to produce c-nets up to order 20, and investigated squared squares up to order 19. Table II (p51) has the results, a listing of simple imperfect squared squares up to and including order 19. No simple perfect squared squares were found. So Duijvestijn and Bouwkamp established that the lowest order simple perfect squared square must be order 20 or higher.
P. Medema is given credit in Duijvestijn's thesis for assistance with programming and debugging.
It was not possible to continue the investigation any further at this time. Duijvestijn had used the processing power, memory and secondary storage of the computing equipment to its limits. As c-nets and squared rectangles increase by order, the number of objects increases exponentially so that the computer hits a wall where it cannot process the volume of data required. Throughout the sixties, many of the discoveries made were based on the tables produced by Duijvestijn and Bouwkamp but using human construction techniques.
Further computer searches, using a different methodology were performed by J. C. Wilson in his 1967 thesis. Collecting and recording the calculations from those searches at a standing computer desk, you can see that he produced simple perfect squares of lower order than previously (order 25), but not a complete catalog and he did not find the lowest order simple perfect squared square.
In 1973 N. D. Kazarinoff and R. Weitzenkamp showed there is no compound perfect square less than order 22, and thus slightly improved Duijvestijn and Bouwkamp's result that the lowest order perfect squared square must be greater than order 20, to being either order 20 or 21 simple, or order 22,23 or 24 simple or compound (Willcocks square is order 24).
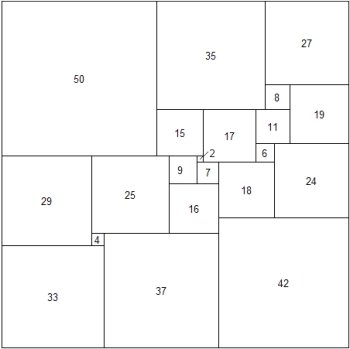
AJWD's order 21 SPSS, 112 x 112
Computer storage and processing power had started to grow according to Moore's Law, pushing the computational limits back, so in 1978 Duijvestijn decided to run his software on current hardware, to continue the search for the lowest order simple perfect squared square. During the night of March 22, 1978 a line of computer output from Duijvestijn's program showed he had found order 21 112x112 (AJWD) the lowest order simple perfect squared square. Imagine the elation Duijvestijn must have felt that night.
Duijvestijn continued his searches and located the lowest order 1 x 2 simple perfect squared rectangle. He also collaborated with Augusteijn on simple perfect squared cylinders of low order.
In 1982, Duijvestijn, Federico and P. Leeuw collaborated in an article about compound perfect squares. The trio was able to meet their main objective, namely, the identification of the lowest-possible order compound perfect square. As many had expected, the lowest possible order compound perfect square was the "little gem of Willcocks", 24: 175 (THW).
Then, in 1990, Duijvestijn decided to start all over again when computer power had again grown tremendously, compared to that of the sixties and seventies. In the early 1990's he systematically searched through orders 21, 22, 23, 24, 25 and 26 and published complete catalogs of all squared squares found.
A former student of the Universirty of Twente, Evert van Dijken has this recollection of Professor Duijvestijn.
I studied Applied Mathematics (Numerical Analysis) at that time and Computer Science was at that time not a separate department. It was also the smallest department (200 students) so everyone knew everyone. I had to compete with Prof. Duijvestijn for the use of the computer, but I never followed a lecture from him. I attended as a student the meeting at the university where Professor Duijvestijn revealed his lowest order simple perfect squared square discovery. Also I remember he very proudly showed a letter there which he got from Martin Gardner. The computer centre of the university was closed in the weekends for students and staff from Friday 18:00 until Monday 08:00 and professor Duijvestijn used the complete DEC-10 computer for the whole weekend. He lived at the campus and regularly checked the computer, coming on his bike, as there was no support in the weekends. I remember that when for the first time the computer centre was also open for students at Friday night Professor Duijvestijn came in expecting that the computer could be used by him, but he had to wait a few hours. And he got personally 99% of the budget for his research group and students for the use of the computer.
A granite monument has been erected at the University of Goettingen, Germany. On the cold, black granite surface is incised the 21st order dissection of AJWD. This mathematical monument is breathtaking. It is at once beautifully simple and stark. It is not only a tribute to AJWD but to every worker who contributed to the body of knowledge in this most collaborative of efforts. Duijvestijn passed away in 1998.

Professor A.J.W. Duijvestijn, on his retirement. Image supplied by Beeldbank of the University of Twente
References
- 'Squared Squares, Who's Who & What's What', p52-54 Jasper Dale Skinner, II, Ph.D.
- C.J. Bouwkamp, A.J.W. Duijvestijn and P. Medema, "Catalogue of simple squared rectangles of orders nine through fourteen and their elements", Technische Hogeschool, Eindhoven, The Netherlands, May 1960, 50 pp
- C.J. Bouwkamp, A.J.W. Duijvestijn and P. Medema, "Tables relating to simple squared rectangles of orders nine through fifteen", Technische Hogeschool, Eindhoven, The Netherlands, Aug 1960, 360 pp (Reprinted January, 1986 EUT Report 86-WSK-03.)
- C.J. Bouwkamp, A.J.W. Duijvestijn and P. Medema, "Table of c-nets of orders 8-19 inclusive", 2 vols. Philips Research Laboratories, Eindhoven, the Netherlands 1970; unpublished available in UMT file of Mathematics of Computation.
- A.J.W. Duijvestijn, Electronic computation of squared rectangles. Dissertation, Technische Hogeschool, Eindhoven, The Netherlands, 1962; also in Phillips Res. Reports 17 (1962) 523-612
- C.J. Bouwkamp, A.J.W. Duijvestijn and J. Haubrich, Catalogue of simple perfect squared rectangles of orders 9 through 18, Philips Research Laboratories, Eindhoven, The Netherlands, 1964 (unpublished) vols 1-12, 3090 pp.
- A. J. W. Duijvestijn, "Algorithmic calculation of the order of the automorphism group of a graph", Technische Hogeschool Twente No 221, Enschede, The Netherlands, (1978)
- A. J. W. Duijvestijn, "Simple perfect square of lowest order", J Comb. Theory Ser. B 25 (1978) 240-243.
- A. J. W. Duijvestijn, P. Leeuw, "Lowest Order Squared Rectangles and Squares With the Largest Element Not on the Boundary", Mathematics of Computation, Vol. 37, No. 155 (Jul., 1981), pp. 223-228
- A. J. W. Duijvestijn, P. J. Federico, and P. Leeuw, "Compound Perfect Squares", Amer. Math. Monthly 89 (1982) pp 15-32
- A. Augusteijn, A. J. W. Duijvestijn: Simple perfect square-cylinders of low order. J. Comb. Theory, Ser. B 35(3): 333-337 (1983)
- A. J. W. Duijvestijn: Simple Perfect Squared Squares and 2 x 1 Squared Rectangles of Orders 21 to 24. J. Comb. Theory, Ser. B 59(1): 26-34 (1993)
- C.J. Bouwkamp and A.J.W. Duijvestijn, Catalogue of simple perfect squared squares of orders 21 through 25, EUT Report 92-WSK-03, Eindhoven, The Netherlands, 207 pp.
- A. J. W. Duijvestijn: The number of polyhedral (3-connected planar) graphs. Math. Comput. 65(215): 1289-1293 (1996)
- A. J. W. Duijvestijn: Simple perfect squared squares and 2 x 1 squared rectangles of order 26. Math. Comput. 65(215): 1359-1364 (1996)