J. C. Wilson
In 1965 William Tutte wrote[3] of research being performed by his Ph D student John C. Wilson;
"A new application of an electronic computer to the problem has been made by J. C. Wilson. He has examined a large number of graphs of about 25 edges, each graph being the union of two polar nets with only their poles in common. The polar nets are taken from Bouwkamp's tables, and the complexities of their combinations are readily computable. Many of the graphs were found to have square complexities, corresponding to the case m = 1 of the theory given in Section 4. These gave rise to several simple perfect squares. One of these squares, of order 25, is shown in Figure 3. Its discovery was announced at the IBM sym- posium held at White Plains, New York, in March 1964.[3]"
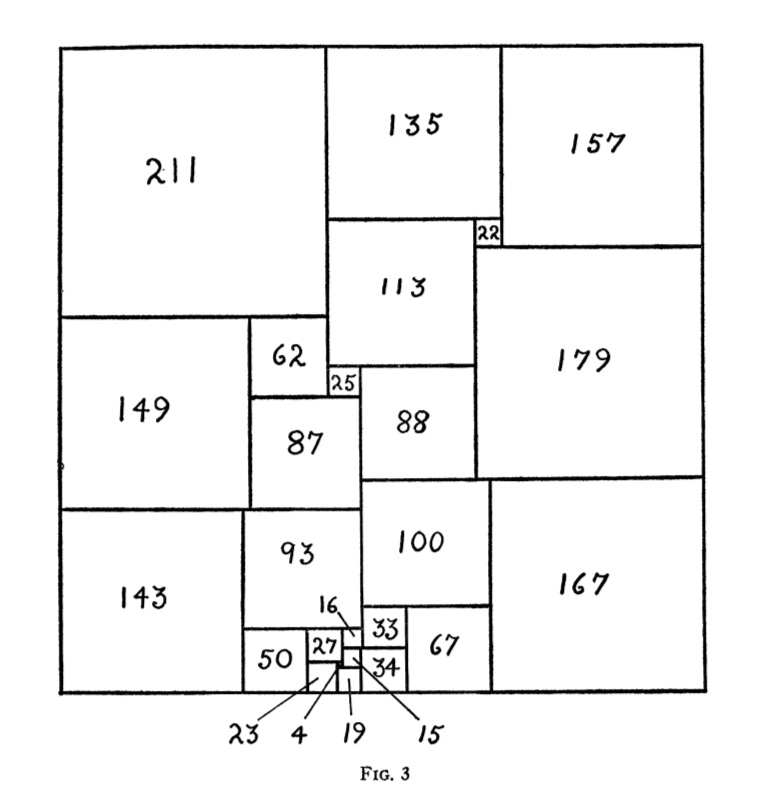
1967 J.C. Wilson published his PhD thesis with 5 new SPSSs of order 25 (including the order 25; side 503 he found in 1964) and 24 new SPSSs of order 26.
J. C. Wilson held the record for the simple perfect squared square with the lowest order known of 25. Wilson held this record from 1964 until 1978 when Duijvestijn found the lowest order simple perfect squared square 21 : 112A "so far, the lowest order simple perfect squares known, are of order 25, the first one of which, due to Wilson, was published in [l]." [2]
An explanation of Wilson's computer assisted method, by Jasper Skinner from his book 'Squared Squares, Who's Who and What's What'; Wilson's method.
- J.C. Wilson, “A Method for Finding Simple Perfect Squared Squarings,” Thesis, University of Waterloo, 1967.
- A. J. W. DUIJVESTIJN, Simple Perfect Squared Square of Lowest Order, JOURNAL OF COMBINATORIAL THEORY, Series B 25, 24&243 (1978)
- W. T. TUTTE, THE QUEST OF THE PERFECT SQUARE, The American Mathematical Monthly, Vol. 72, No. 2, Part 2 (Feb., 1965), pp. 29-35
- Jasper Dale Skinner II, 'Squared Squares, Who's Who and What's What' (1993), pp. 56-65