Roland Percival Sprague (1894-1967)
Some 10 years after Zbigniew Moroń had first published the lowest order simple perfect squared rectangle, the question of the possibility of a simple perfect squared rectangle was only just raised in Germany. Two years later, Zbigniew Moroń's discovery was cited as the answer to this question in a paper by Jaremkewycz, Marenholz and Sprague (1937)[1]. So Sprague knew of the problem by at least 1936 and Zbigniew Moroń's work, once virtually unknown, was now widely known.
In 1938 Roland Sprague found a solution to the problem. Sprague constructed his solution using several copies of various sizes of Zbigniew Moroń's Rectangle I (33x32), Rectangle II (65x47) and a third 12 order simple perfect rectangle and five other elemental squares to create an order 55, compound squared square with side 4205.
Roland Sprague published his discovery prior to Brooks, Smith, Stone and Tutte and is credited with finding the First Squared Square.
P. J. Federico has provided a diagram which shows the structure of Sprague's square.
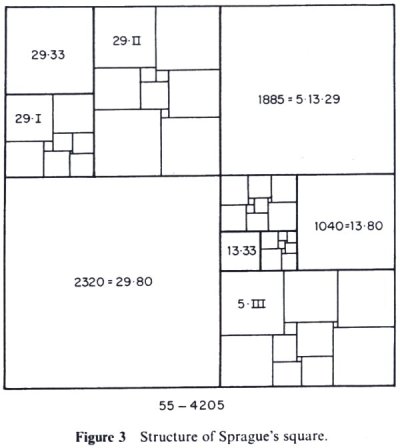
It is interesting that that the first publised squared square used the first two published lowest order simple perfect squared rectangles by Moroń. Tutte noted the construction could be simplified. Like the Trinity Four solutions, Sprague's solution is intricate and ingenious, but unlike their method is not based on a general method, but he published his solution to the problem first.
References
- Jaremkewycz, Mahrenholz and Sprague, Answer to problem 1242, Z Math. Naturwiss. Unterricht Schulgattungen 68 (1937) 43; Proposed in 66 (1935) 251
- Alfred Stöhr, 'Über Zerlegungen von Rechtecken in inkongruente Quadrate', Schr. Math. Inst. Angew. Math. Univ. Berlin 4, Part 5 (1939) 118-140.
- R. Sprague, 'Beispiel einer Zerlegung des Quadrats in lauter verschiedene Quadrate', Math. Z. 45 (1939) 607-608.
David Moews has provided an English translation of this paper on his website. A pdf of the paper is here. - R. Sprague, 'Über die Zerlegung von Rechtecken in lauter verschiedene Quadrate', J. Reine angew. Math. 182 (1940) 60-64
- R. Sprague, 'Zur Abschätzung der Mindestzahl inkongruenter Quadrate, die ein gegebenes Rechteck ausfüllen', Math. Z. 46 (1940) 460-471.
- 'Squared Squares, Who's Who & What's What', p14-49 Jasper Dale Skinner, II, Ph.D.
- 'The Dissection of Rectangles into Squares', R. L. Brooks, C. A. B. Smith, A. H. Stone and W. T. Tutte, Duke Mathematical Journal 7, no. 1 (1940), p 312–340