Order 24 CPSS

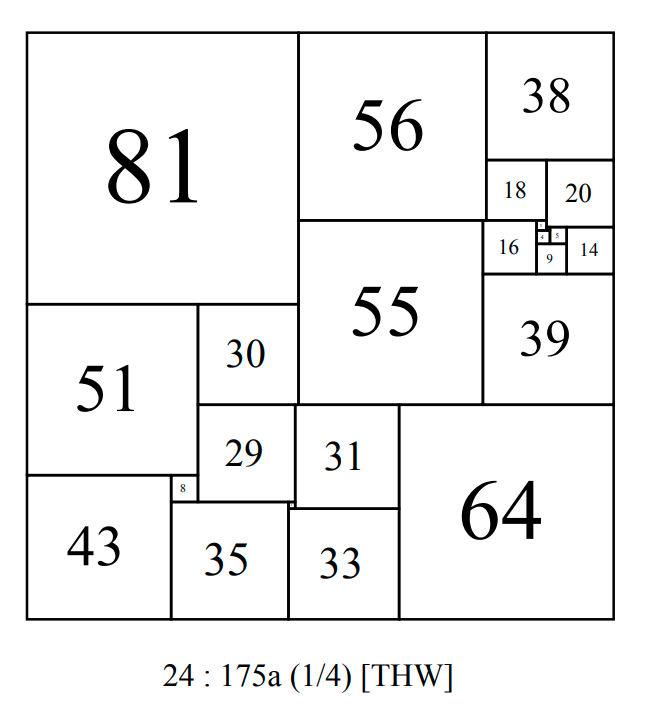
In October 1948 T.H. Willcocks, published his discovery of a compound perfect squared square (CPSS) in the Fairy Chess Review, [1], with a side of 175, composed of 24 different squares (order 24). It held the record as the smallest known size and lowest order perfect squared square for the next thirty years, and was eventually found to be the smallest size, lowest order CPSS and the single CPSS of that order. It was constructed by overlapping two squared rectangles, one perfect and the other containing a single trivial imperfection involving a corner square. Willcock's CPSS 175 order 24 has 4 isomers (4 ways that the internal 94x111 squared rectangle can be oriented within the square).

CPSS 175 order 24 bouwkampcode

CPSS 175 order 24 tablecode

(1) CPSS 175 Order 24 cpsso24.pdf

(4) CPSS 175 Order 24; isomers cpsso24-isomers.pdf