'Special' Perfect Squared Squares
'Special' Perfect Squared Squares are Perfect Squared Squares, which have some features or property which makes them 'special'.
DEFINITIONS: A squared rectangle is a rectangle dissected into a finite number, two or more, of squares, called the elements of the dissection. If no two of these squares have the same size the squared rectangle is called perfect, otherwise it is imperfect. The order of a squared rectangle is the number of constituent squares. The case in which the squared rectangle is itself a square is called a squared square. The dissection is simple if it contains no smaller squared rectangle, otherwise it is compound. Simple Perfect Squared Squares are SPSSs, Compound Perfect Squared Squares are CPSSs, a Perfect Squared Square can be an SPSS or a CPSS and is a PSS. Simple Imperfect Squared Squares are SISSs, Simple Perfect Squared Rectangles are SPSRs, and so on ...
Among the characteristics which mark PSSs as being 'special' are items in the following list;
- Lowest Order PSS (Perfect Squared Square)
- Smallest size PSS
- Smallest Size PSS per Order
- Largest Size PSS by Order
- Maximum Element Size by Order
- Maximum Element Size as a Proportion of the PSS Size
- Crossed PSSs
- Perfect Squared Square Isomers
- Disjoint N-tuples
- 'Nice' Perfect Squared Squares
- Maximum Number of Largest Elements Not On the Boundary (and Not in Corners)
- Minimum Number of Boundary Elements in a PSS (7)
- Maximum Number of Boundary Elements in a PSS (>50%)
- Minimum Size (5) of Boundary Element in a PSS
- Minimum Corner Element Size in a PSS
- The Maximum and Minimum Number of Prime Elements in a PSS (by Order), and the distribution of Prime Elements in PSSs.
- Element Parity Counts in PSSs
- Element Situated at the Center of a PSS
- References
Lowest Order PSS (Perfect Squared Square)
For many years the lowest order PSS was the 'Holy Grail' of squared square research. The lowest order PSS was discovered in a computer search by Duijvestijn in 1978. By 'lowest order' we mean the squared square with the fewest squares. The 'order' is the number of squares in the dissection. The squared square must be 'perfect', that is, no two squares are the same size.
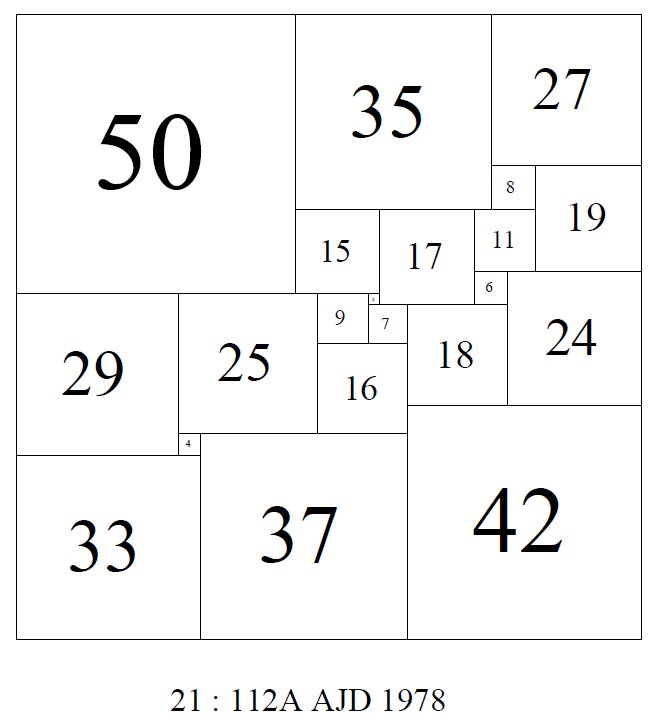
Duijvestijn's order 21 SPSS (simple perfect squared square) is unique, it is the only SPSS of order 21, and order 21 is the only PSS order with a count of one. A common misconception about the lowest order PSS is that it is also the smallest PSS. It is not. Duijvestijn's order 21 SPSS has a side of 112. There are SPSS of higher order, but which have a smaller side than 112. They are the next entry in our list of Special Squared Squares.
Smallest size PSS
The smallest PSS size is 110. There are 3 SPSSs with a side of 110.
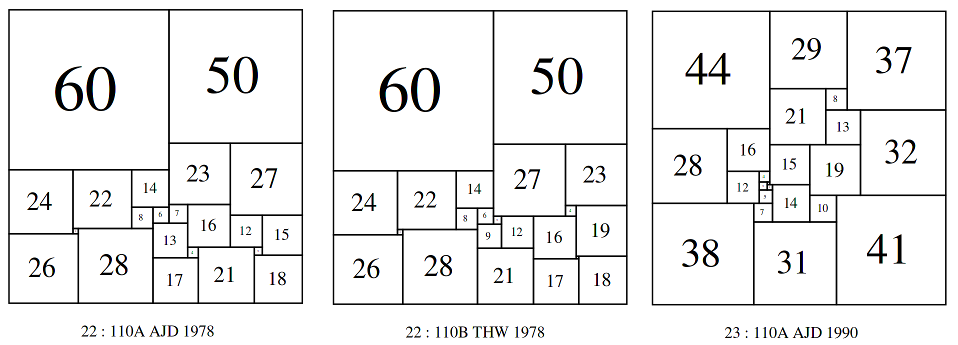
Bouwkamp wrote in 'Catalogue of Simple Perfect Squared Squares of orders 21 through 25'
"The very first Simple Perfect Squared Square of this Catalogue was discovered by computer in March, 1978, by Duijvestijn. It has the lowest possible order, n = 21, and it is the only one of that order. In July of the same year, Duijvestijn found two simple perfect squared squares of order 22. After communicating these to P.J. Federico of Washington, D.C., U.S.A., who informed T.H. Willcocks of Bristol, U.K., the latter found a third simple perfect squared square of order 22 about August 1978."
Later, in 'Album of Simple Perfect Squared Squares of order 26 by C.J. Bouwkamp and A.J.W. Duijvestijn' Bouwkamp gave some more intriguing details of the discovery of the Willcocks 110;
"These two squares were sent to Federico, who in turn communicated them to Willcocks. When Willcocks studied 22:110, in trying to find the rectangular generators of the square in the sense of Wilson, he "was listening to the broadcast news and my mind was less than half on this problem so, in error ... found '" a second square" and he continues "This goes to show that even stupidity may sometimes yield a useful result". That is Willcocks's story of the birth of 22:110 by serendipity. It is a pity that details of Willcocks's analysis have not appeared in print."
I would regard Bowkamp's characterisation of the Willcocks discovery with the word 'serendipity' to be preferable and more accurate than 'stupidity'. The third SPSS with size 110, or order 23 was discovered some years later; Bouwkamp writes;
"Then, in 1990, Duijvestijn decided to start all over again when computer power had tremendously grown compared to that of the sixties. He first found eight simple perfect squared squares of order 22, including his earlier two. Secondly, he found twelve of order 23 and twenty six of order 24."
Among the twelve order 23 SPSSs was another with a side of 110.
How do we know these three 110 size PSSs are smallest? This is an interesting question, considering the existence of these 3 110 SPSSs (2x 22:110 and 23:110), alongside the 21:112 SPSS, shows that perfect squared squares at a higher order can have a smaller size than those at a lower order. There are several proofs that these are the smallest PSSs. Before we go to the proofs, it is instructive to eliminate some other possibilities which were thought to be possible candidates for the smallest perfect squared square. One of these was based on the curious fact that 12+22+32+...+242 = 702. We can show this is true using the sum of squares formula for the first n integers and making it equivalent to a square number, i.e. S2 = n(n + 1)(2n + 1)/6. Solutions to the formula n(n + 1)(2n + 1)/6 are the pyramidal numbers. The first few pyramidal numbers are: 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819 (sequence A000330 in OEIS). Solving the diophantine equation, S2 = n(n + 1)(2n + 1)/6 involves finding a pyramidal number which is also a square number, this is a known problem, the Cannonball Problem, and was solved in 1918 by Watson. The only solutions in integers for (n,S) are (1,1) and (24,70). The trivial solution (1,1) corresponds to the unit square, and it was conjectured that the squares 1 to 24 might tile a square of size 70. If this were true there would exist an order 24 perfect squared square (PSS) of size 70. However Martin Gardner wrote in his book Mathematical Carnival, that in 1974 two computer scientists at the University of Illinois at Urbana-Champaign, Edward M. Reingold and James Bitner, wrote a program to solve this problem and with it they proved that such a tiling was not possible. This result was later confirmed by Duijvestijn's enumeration of order 24 SPSSs in 1991 and Duijvestijn, Federico and Leeuw's enumeration of order 24 CPSS in 1980.
Another possible candidate for the smallest perfect squared square was thought to be T.H. Willcocks 1948 discovery of the order 24, side 175 compound perfect squared square (CPSS). This is the lowest order and smallest size CPSS, and held the record for the smallest PSS for thirty years, but the discovery of the size 110 SPSSs shows it is not the lowest order and smallest size PSS. Ironically Duijvestijn's discovery of the first 110 beat Willcock's record for the smallest PSS, but Willcock's serendipitous discovery of the other 110 of order 22 ensured he was able to quickly regain and hold that record equally with Duijvestijn forever.
In 1999 Ian Gambini presented his thesis (French) and proved, using a tiling decomposition algorithm, that the smallest perfect squared square is 110 in size, and that there are three distinct solutions (ignoring symmetries), being those discovered by Duijvestijn and Willcocks. See "A method for cutting squares into distinct squares", Ian Gambini, Discrete Applied Mathematics 98 (1999) 65–80 for an English translation featuring this result.
Despite the negative result for tiling 702 we can use the equation S2 = n(n + 1)(2n + 1)/6, to get lower bounds on the size of a PSS by order. For a PSS to be as small as possible we need to minimise the size of the squares in the dissection, and minimise the difference in sizes between squares, while ensuring that none of them are the same size. This can be done by using consecutive integers starting at 1. No PSS could be smaller in size than the square root of the sum of the square of the first n integers where n is the order, because consecutive integers have the smallest difference (a difference of 1) between successive integers, and consecutive integers starting at 1 are the smallest possible set of n integers in different sizes from a set of all possible different n integers. We can use the sum of squares formula to find the 33rd pyramidal number (or just sum the squares of the first 33 integers), it is 12529. The square root of 12529 is approximately 111.93. So a PSS with a side less than 112 could not have more than 32 squares. Conversely if any PSSs with less than a side of 112 exist, they could only exist in orders 21 to 32. (Duijvestijn proved that no PSSs exist below order 21, and this fact has been confirmed many times since). As of September 2013 PSSs of orders 21 to 32 were completely enumerated by Lorenz Milla and Stuart Anderson, all 2-connected planar graph embeddings up to 33 edges and with minimum degree 3 vertices were produced with plantri, transformed into electrical networks and then translated to squared tilings with squared squares extracted. The smallest PSSs found were the 3 known SPSSs with a size of 110. This provides another proof of Gambini's result that 110 is the smallest possible size for a PSS.
Smallest Size PSS per Order
The smallest PSSs of each order from 21 to 37 are 112, 110, 110, 120, 147, 212, 180, 201, 221, 201, 215, 185, 233, 218, 225, 253, 237. (This is OEIS sequence A217148 - this sequence has the same entries as A129947 but A129947 is SPSSs only. Based on James Williams work the best known values for orders 38 to 39 are; 352, 360. These terms have a size/order measure ranging from 4.782 for the 23:110 SPSS, 5 for the two 22:110s and 24:120, up to 9.23 for 39:360. By this measure 23:110 is both the smallest known PSS in relative terms by size/order and in absolute terms by size. A pdf of the SPSS dissections for A129947 is here.
The sum of squares formula gives a lower bound for the size of the smallest PSS of each order.
Largest Size PSS by Order
As the PSS order increases, the element sizes increase, and the sizes that are possible for PSSs increase also. This is consistent with Kirchhoff's Matrix-Tree theorem, when applied to the graphs underlying squared squares and squared rectangles. As the number of edges in the graph class increases, so does the number of spanning trees, and from that the dimensions of the dissection and the sizes of the elements. Also as the graphs from which PSSs can be derived belong to finitely generated classes, we can conclude that the number of PSSs in a given order are also always finite, and therefore there is always going to be a largest size for any particular order of PSSs. The largest possible PSSs of each order from 21 to 37 are known as these orders have been completely enumerated. They are; 112, 192, 332, 479, 661, 825, 1179, 1544, 2134, 2710, 3641, 4988, 6391, 8430, 11216, 15039, 20242. They are all SPSSs. This is OEIS sequence A217149. A pdf of the SPSS dissections for A217149 is here.
An upper bound for PSS size by order can be obtained from factoring the maximum determinant (equivalently the number of spanning trees) of the graph class. Brooks, Smith, Tutte and Stone (1940) [2] proved (6.12) THEOREM. Let the full sides of a p-net be H, V. Then the reduction p is a multiple of the upper square root of the H.C.F. of H and V.
In 1965 Tutte wrote[7], "Let G be a 3-connected planar graph. It is known that such a graph can be drawn in the 2-sphere,or closed plane, in essentially only one way ([9], [10]). Let A be an edge of G, with ends x and y, and let P be the graph obtained from G by deleting the edge A. We use Kirchhoff's equations to obtain the currents in P on the assumption that the total current enters at x and leaves at y, and that the edges of G are unit resistances. It is shown in [2] that the resulting distribution of currentsin P determinesa squared rectangle R. Usually P is the horizontal polar net of R, though this rule breaks down when P has a zero current,or when two vertices of P, not separated by G in the 2-sphere,have equal potentials. Every simple squared rectanglecan be derived,however, from its horizontal c-net by applying the above construction to the appropriate edge A. It follows from the above considerations that all simple squared rectangles of the nth order can be determined provided that we can first list the 3-connected planar graphs of n+1 edges.
In the determination the currents in P it is convenient to take the total current equal to the complexity C(P) of P. This is the number of spanning trees of P, that is the number of subgraphs of P which are trees and which include all the vertices of P. With this convention it is found that the currents in P are all integers. We describe these currents and the correspondings potential differences in P as full. The reduced currents obtained from full ones by dividing by their highest common factor. It is the reduced currents that are the side-lengths of the constituent squares of R "in its lowest terms."
The full potential drop from vertex a to vertex b when the total current enters P at x and leaves at y is conveniently denoted by (ab.xy). it can be regards as a function of P or G, for it takes the same value in each network.
Let G be any network of unit resistances,let C be its complexity,and let a, b, x and y be vertices of G. Then it is shown in [2] that (ab.ab)(xy.xy) -(ab.xy)^2 mod C. If G is the polar net, with poles x and y, of a squared square S we have C = (xy xy). Writing C = mk2,where m is square-free, we find that mk divides (ab.xy). Thus to find the reduced currents corresponding the squares of S divide the associated full currents by the large reduction factor mk".
Let G be a planar graph with n vertices. The number of spanning trees of G is at most O(5.28515^n) . If G is 3-connected and contains no triangle, then the number of its spanning trees is bounded by O(3.141619^n). If G is 3-connected and contains no triangle and no quadrilateral, then the number of its spanning trees is bounded by O(2.71567^n). See http://arxiv.org/abs/0912.0712
Using bounds on the number of spanning trees s(T) by vertex, and then taking the square root of s(T) were obtain a bound for squared square maximum size across a range of orders with that number of vertices and a varying edge number (and corresponding range of orders). the bounds obtained are much heigher than the maximum found in enumerated orders.
Maximum Element Size by Order
The largest possible elements of each order of PSS from 21 to 32 are; 50, 97, 134, 200, 343, 440, 590, 797, 1045, 1435, 1855, 2505, 3296, 4528, 5751, 7739, 10361. They are all from SPSSs. This is OEIS sequence A228953. A pdf of the SPSS dissections for A228953 is here.
A upper bound on element size by order can also be obtained from the maximum determinant (equivalently the number of spanning trees) as above in the Largest Size PSS by Order. See Triangled Equilateral Triangles, the section on the Matrix-Tree theorem for an explanation on how element sizes can be calculated.
Maximum Element Size as a Proportion of the PSS Size
How large can an element be as a proportion of the PSS size? Among the complete orders 21 to 32 the best is an element a little over 2/3rds (66.7%) of the size of the PSS. This pdf has the best result in each order from 21 to 32.
We can do much better, it should be possible to construct CPSSs so that the largest element approaches 100% of the size of the CPSS. The trick is to create 2 long thin, simple perfect squared rectangles (SPSRs) with particular ratios, join them at right-angles and then add an large extra square in the remaining space. For example Brian Trial has created 1xn SPSRs from n = 4 to 18. Creating 1xn SPSRs is a natural generalisation of the squared square problem (which is 1xn, n=1) and is quite difficult to do. Brian's results on this problem are extraordinary.
Two pdfs of Brian's 1xn SPSRs are here;
(landscape version) and (portrait version). By scaling and fitting Brian's 1x17 and 1x18 SPSRs and adding one extra square, equal to the size of the long side of the scaled 1x17 rectangle, a compound perfect squared square (CPSS) is created with the largest element square having a side equal to 94% of the CPSS side. A pdf of this CPSS (order 560; size 338321736) has been constructed. The smaller elements are dwarfed by the larger square, you need to zoom in to see them along the sides.Crossed PSSs
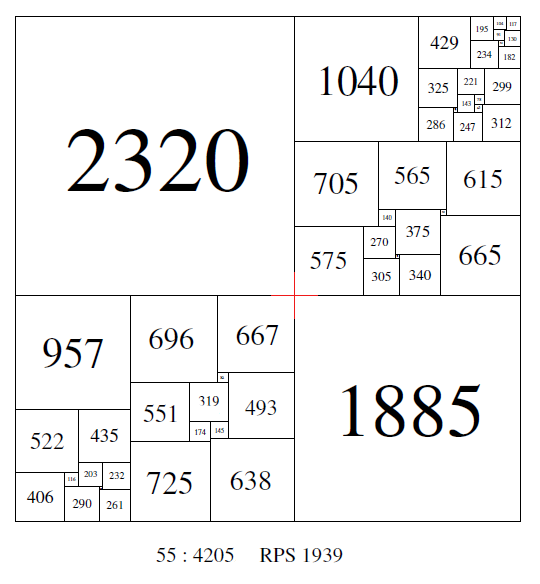
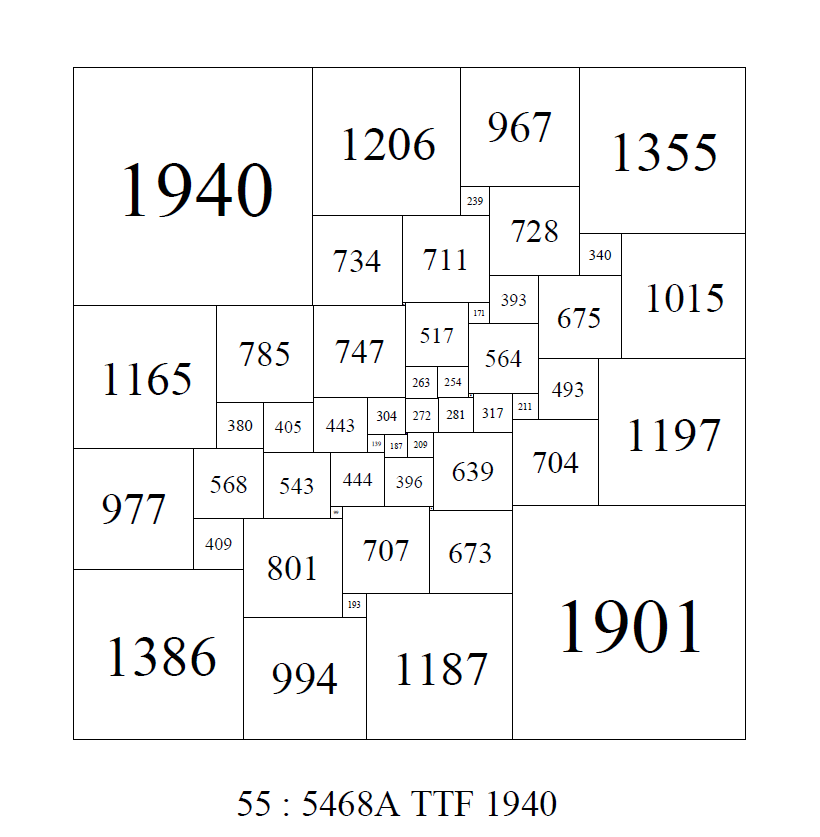
Some the earliest known perfect squared squares featured crosses in their construction. For example, Sprague's square of order 55, side 4205. This PSS also deserves mention as 'special' for being the first PSS published.
A order 38 compound perfect squared square found by Roland Brooks, using the rotor-stator symmetry method, has 2 crosses;
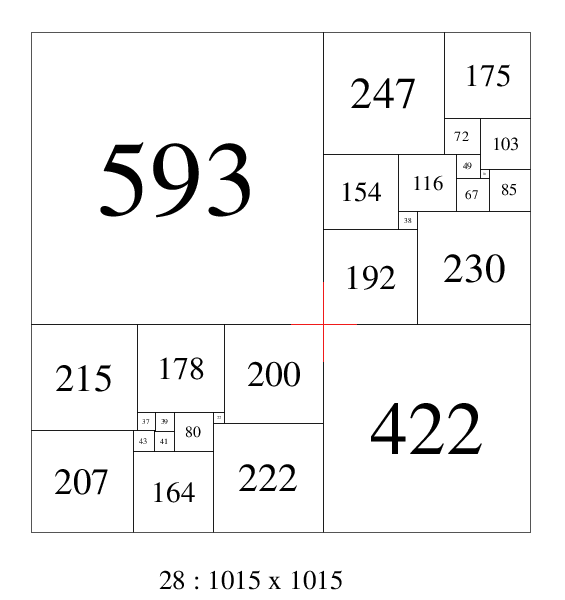
A order 28 compound perfect squared square found by Arthur Stone, using 2 order 13 simple perfect squared rectangles, and 2 additional squares, has a cross. This is the R1, R2 Moron construction and is a crossed construction;
In Brooks, Smith, Stone, Tuttes 1940 paper "The Dissection of Rectangles into Squares" they referred to an order 55 SPSS created using advanced rotor stator techniques. The square had no cross and this was regarded as an achievement. The cross being regarded as a 'blemish', indicative of the construction, which should be eliminated where possible, although it was quickly realised that Perfect Squared Squares with crosses were quite a rare phenomena.
Duijvestijn recorded the bouwkampcode and the orders in which crosses first appeared. In order 26 he found the first SPSS with a cross of lowest order[1]. He also found the lowest order CPSS with a cross in order 26. With CPSSs one needs to examine all the isomers of a CPSS, as some isomers may be crossed, and other isomers of the same CPSS are not. The lowest order SPSR and SISR with a cross are in order 17 and and the lowest order SISS with a cross is in order 18. I have extended the counts a little further to order 21 for simple perfect squared rectangles and to order 32 for perfect squared squares.
THE NUMBERS OF CROSSED SQUARED RECTANGLES AND SQUARED SQUARES
Order SPSR
SISR
SPSS
CPSS (isomers)
SISS
CPSR
9
-
-
-
-
-
-
10
-
-
-
-
-
-
11
-
-
-
-
-
-
12
-
-
-
-
-
13
-
-
-
-
-
14
-
-
-
-
-
15
-
-
-
-
-
16
-
-
-
-
-
17
2
5
-
-
-
18
2 8
-
-
2
19
7 36
-
-
-
20
29 72
-
-
10
21
166
-
-
4
22
-
-
58
23
-
-
57
24
-
-
366
25
-
-
351
26
1
1
1858
27
3
-
1998
28
10
18
29
23
15
30
71
122
31
146
231
32
338
1190
Perfect Squared Square Isomers
In squared rectangles and squared squares, an isomer is a squared tiling or dissection which is of same size and dimensions as another tiling, with all elements pairwise the same, but arranged differently. All CPSSs exist as isomers, due to the subrectangles being oriented in different ways. SPSS isomers are considered special as the isomerisms are rarer and each is a different configuration. Isomers are an important design ingredient for puzzles made from the elements of Perfect Squared Square. The ability to put the pieces together in completely different ways makes for an interesting puzzling problem.
Isomers have an important historical role to play in the research conducted by Brooks, Smith, Tutte and Stone.
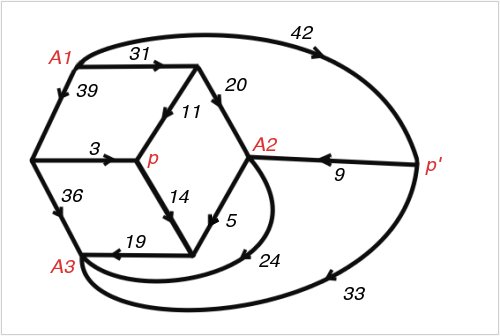
Figure 74; 112 x 75A Smith Diagram
Tutte wrote,
"It was a pleasing recreation to work out perfect rectangles corresponding to networks with a high degree of symmetry. We considered, for example, the network defined by a cube, with corners for terminals and edges for wires. This failed to give any perfect rectangles. However, when complicated by a diagonal wire across one face, and flattened into a plane, it gave the Smith diagram of Figure 74 and the corresponding squared rectangle of Figure 75. This rectangle is especially interesting because its reduced elements are unusually small for the thirteenth order. The common factor of the elements is six. Brooks was so pleased with this rectangle that he made a jigsaw puzzle of it, each of the pieces being one of the component squares."
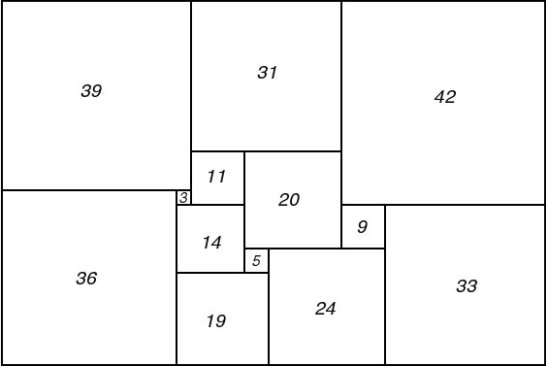
Figure 75; 112 x 75A Squared Rectangle
"It was at this stage that Brooks's mother made the key discovery of the whole research. She tackled Brooks's puzzle and eventually succeeded in putting the pieces together to form a rectangle. But it was not the squared rectangle which Brooks had cut up! Brooks returned to Cambridge to report the existence of two different perfect rectangles with the same reduced sides and the same reduced elements."
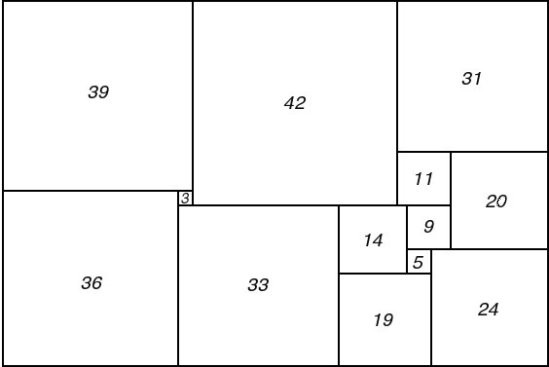
Figure 76; 112 x 75B Squared Rectangle
The phenomena of isomerism led Brooks, Smith, Tutte and Stone to examine the electrical networks of the two rectangles, they found they were related by symmetry. Further exploration of symmetry led to networks which could produce rectangles of the same size with all elements different (or with a single corner element the same), these can be assembled, with 2 other squares, to form a compound perfect squared square.
The 112 x 75 rectangles in Figures 75 and 76 reappear in CPSS isomers of order 30, there are 2 CPSS of order 30, side 629 with the same elements, each CPSS has one of the 112 x 75 SPSRs as a subrectangle.
Duijvestijn cataloged isomers. In order 25 SPSS he found 3 pairs of isomers [1].
Isomers can be classified by the number in each class;
Two – pairs, Three – triples, Four – quadruples, Five – quintuples, Six – sextuples, Seven – septuples, Eight – octuples, Nine – nonuples, Ten – decaples, Eleven – undecaples, Twelve – duodecaples, Thirteen – tridecaples, Fourteen – quadecaples, Fifteen – quindecaples, Sixteen – sexdecaples, Seventeen – sepdecaples, Eighteen – octdecaples, Nineteen – nondecaples.The following counts are a final tally of sorted adjacent isomers by order
CPSS always exist as isomers, the number of isomers in each order is shown, along with the number of CPSS equivalence classes for each order. The number in CPSS (classes) is the number of isomers between CPSS equivalence classes. It is also possible for simples and compounds of the same dimensions and order to form isomers.THE NUMBERS OF SQUARED RECTANGLE AND SQUARED SQUARE ISOMERS
Disjoint N-tuples
Disjoint N-tuples can be regarded as the opposite of isomers, instead of looking for same size tilings where all the elements are the same in each tiling, but arranged differently, which is the case for isomers, we are looking for same size tilings, usually with same number of elements, but where there is no element in common.
If A and B are two sets and the intersection of the elements of A and B is the empty set; A ∩ B = ∅, then we can say the elements of A and B are disjoint. An n-tuple is really another name for a list of numbers, in this case we are referring to the elements of a dissection. Perfect Squared Squares (PSSs) A and B can be compared to each other by their element sizes, as can SPSRs A and B of the same shape. If A and B are rectangles, and are the same shape then the height and width of the rectangles are in the same ratio, but they may not be the same size, if this is the case, then we can scale A and B to the same sizes before comparing elements to see if they are disjoint.
The reason we may want to seek out disjoint n-tuples (with SPSRs in particular) is that they provide the necessary ingredients of a well known method for constructing Compound Perfect Squared Squares (CPSSs).
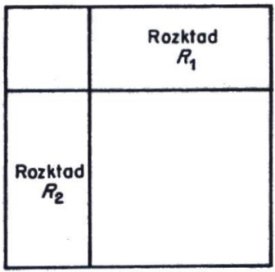
Moroń's figure
In 1925 Zbigniew Moroń [1] raised the question “For what squares is it possible to dissect them into squares?” He then observes “if there exists a rectangle (of different sides) for which there are two dissections R1 and R2 such that; in neither of these dissections does there appear a square equal to to the smaller side of the rectangle and, each square of dissection R1 is different from each square in dissection R2, then the square is dissected into squares, all different, as shown in the following figure.”
In 1940 Arthur Stone [3] published the discovery of a CPSS of side 1015 and order 28 using the Moroń construction. It was constructed from 2 disjoint n-tuple SPSRs of order 13, augmented with two additional squares, equal in size to the respective side lengths of the rectangles. Order 13 is the lowest order in which such disjoint n-tuples appear. Disjoint n-tuple SPSRs of the same size appear in all higher orders of SPSRs in exponentially increasing numbers. From orders 13 to 21, the number of same size disjoint SPSR pairs are 1, 2, 7, 60, 225, 1208, 5186, 20116, 82227. From these pairs an equivalent number of CPSSs can be constructed. In fact even more CPSSs can be created; if 3 SPSRs are a disjoint triple then 3 CPSSs can be produced rather than just two pairs of CPSSs and similarly 6 CPSS can be produced by using 2 pairs at a time from disjoint quadruple SPSRs and so on. Yet even more CPSS can be produced from disjoint quadruples by using all four SPSRs at once. Additional CPSSs can also be produced by comparing SPSRs across orders and by comparing SPSRs of the same shape. The order of the CPSSs produced with 2 SPSRs is double the order of the SPSRs plus 2.
In 2012 Anderson has created large numbers of CPSSs in orders 36 to 42 by combining disjoint n-tuple SPSR orders up to 20.
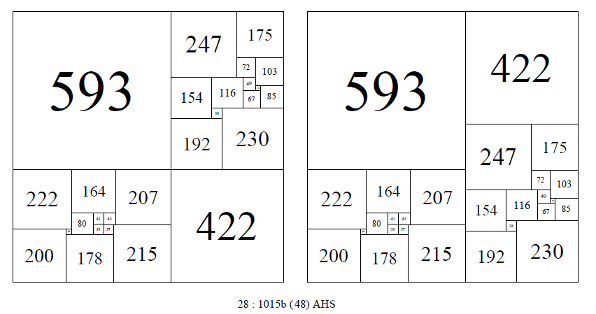
Two of the 48 isomers of 28: 1015b. Arthur Stone (1940)
Each CPSS created from a disjoint pair in this manner can be arranged in 48 isomer classes. The 48 isomer classes can be split into 2 subclasses of 16 and 32, where the two rectangles can be arranged by rotation and reflection in place and also swaps with each other.
A special case exists where two 1x2 SPSRs (of the same size, or scaled to the same size) can be combined along the long side to form a CPSS without the addition of the two extra squares. Three 1x3 SPSRs can be similarly combined to form a CPSS (but only 1 1x3 SPSR is known)
In 1990 Jasper Skinner [4] reported the existence of two unique compound perfect dissections of a square of reduced side 1429 into 29 unequal squares. He wrote,
'To be termed “uniquely squared” two or more perfect squared squares (or rectangles) must meet three criteria:
(1) be of the same order,
(2) have equivalent corresponding reduced sides, and
(3) have no element in common.
Many pairs of perfectly squared squares are known but have common elements. Pairs of uniquely squared simple perfect rectangles of common reduced sides and order first appear at order 13. The low order pair of simple perfect rectangles was completely described by A. H. Stone (1940) [ 3] Triplets of common reduced sides and order first appear at order 16 as indicated by C. J. Bouwkamp (1965) . Special thanks are extended to C. J. Bouwkamp for permission to publish his triplet discovery. The Bouwkampcode of the low order triplets of reduced side ratio 2393:3218 reads as follows:
(A) (1242,627,548, 801) (79,469) (706) (216,585) (316,369) (1151,91) (1060, 53) (1007);
(B) (1243, 1091,884) (207,677)(245,583,470)(1150,93)(338) (315,832)(719,202)(517);
(C) (1273,708, 1237) (312,396) (228,84) (347, 133) (214, 1156) (25,203) (1120, 178) (942).
At present, no quadruplet example of uniquely squared simple perfect rectangles of common reduced sides and order is known. However, C. J. Bouwkamp (1965) has discovered a pair of quadruplets with no common element though the reduced sides differ and the order ranges from 17 to 18."A quadruplet of 4 SPSRs of uniquely squared simple perfect rectangles of common reduced sides and order has been found in order 20. The SPSRs have been combined and are displayed in the Squared Windmill shown further down the page.
Disjoint n-tuple Squared Squares
Skinner constructed the first pair of uniquely squared squares of common reduced side and order.
"These dissections were discovered empirically on May 4-6, 1990 using a technique of T. H. Willcocks (1951) [5, Technique 2.211 applied to two compound perfect squares of 28th-order: the first of reduced side 1015 due to A. H. Stone (1940) [3] and the second of reduced side 1073 described by W. T. Tutte (1950) [6]. The result was a pair of 29th-order compound perfect squares of reduced side 1429 with no common element. The Bouwkampcode of the first reads as follows:
(414,280, 372, 363)(188,92) (93,270) (119,261,84) (199,215) (177) (165,23) (142) (183, 16)(167,47,17) (13,43, 163,796) (30) (120) (633).
The Bouwkampcode of the second is;
(356,244, 153,248,169,259)(91,62) (79,90) (29,33) (364) (360)(349) (111,89, 156) (22,67) (133) (88, 135) (221) (39, 213,821) (174)(608)."Disjoint n-tuple SPSSs first appear in order 26, there are 2 pairs, one of size 752 and one of size 759. Both were discovered by Duijvestijn. The 1429 CPSS pair of order 29 discovered by Skinner is the lowest order in which they appear in CPSSs. There is also another pair in order 29 CPSSs, with a side of 1488. One member of the pair was discovered by Skinner, the other by Anderson and Johnson.
THE NUMBER OF PERFECT SQUARED SQUARE DISJOINT N-TUPLES
Order SPSS
CPSS
21
-
-
22
-
-
23
-
-
24
-
-
25
-
-
26
4;
2 pair
-
27
57;
26 pairs
1 triple (3 x 27:1012)-
28
180;
-
29
784;
4;
2 pairs;
(2 x 29:1429 & 2 x 29:1488)30
2794;
16;
31
9084;
122;
32
29982;
724;
Disjoint n-tuple PSSs can be used to construct other PSSs. For example 2 pair of disjoint n-tuple PSSs, if they are the same size and order, can be placed together in a 2 x 2 arrangement to make a CPSS of twice the size and four times the order, or we can use one pair of disjoint n-tuple PSSs, (same size) and a 1 x 2 SPSR, (both the PSSs and SPSR may need to be scaled), and if no two elements are the same after scaling, we have a new PSS. Or we can use a disjoint n-tuple triple and one extra size square, the size of the PSSs, to make a 2 x 2 PSS construction. Two disjoint n-tuple 1 x 2 SPSRs can be scaled and fitted together to form a PSS. Four disjoint n-tuple PSS (or SPSRS) can be scaled and fitted together to form a PSS. Many other possibilities exist.
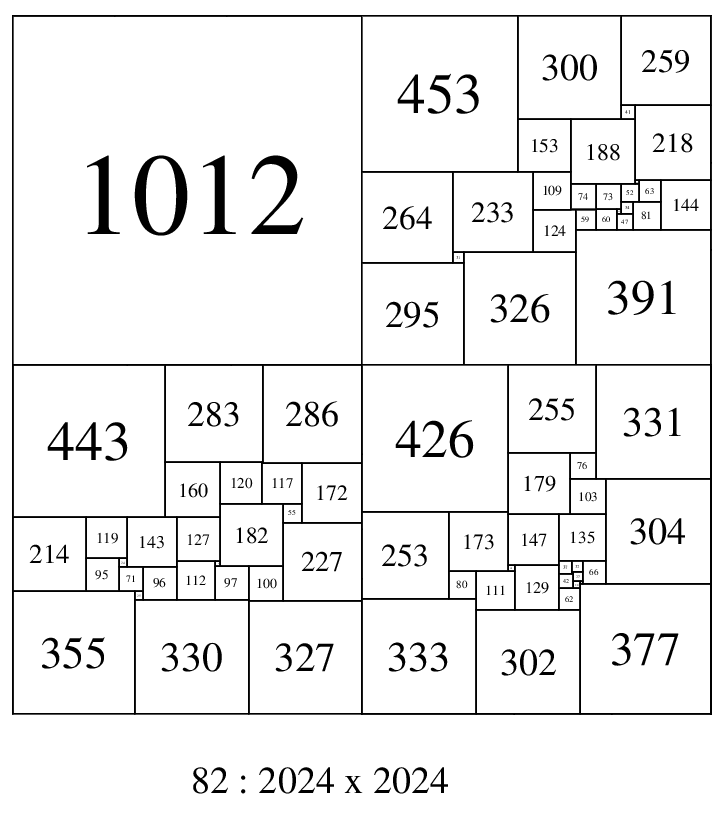
Squared 2 x 2, o82 : 2024 , composed with 3 disjoint n-tuple o27:1012 SPSSs
Squared Windmill
As alluded to above, if one has four disjoint n-tuple SPSRs then a variety of new CPSS constructions are possible. These are extensions of the Moroń construction and its isomers along with a new construction, the Squared Windmill. A squared windmill has 4 rectangles arranged around a central square (equal in size to the difference of the width and height of the rectangles), rather like a windmill.
It is not known what is the lowest order appearance of quadruple disjoint n-tuple SPSRs in the same order. However it is known (Anderson 2011) that a quadruple of disjoint n-tuple SPSRs exists in order 20. A windmill has been created from this quadruple;

Squared Windmill, o81 : 6062 SEA (2012)
'Nice' Perfect Squared Squares
A PSS is 'nice' if the difference in size between the smallest and the largest element (or the smallest element and the PSS side length) is minimised. PSSs that are 'nice' are one of the most popular categories of 'Special' PSSs. There is a perceptible aesthetic associated with 'niceness' which most people respond positively to when viewing 'nice' dissections. There is also a practical quality to 'niceness' as well. Applications of PSSs to the manufacture of objects such as 3D prints, dissection puzzles, quilts, stained glass windows and bookshelves require a criteria of 'niceness' to avoid the impracticability of relatively tiny elements which are a feature of the overwhelming majority of PSSs. Puzzle makers also have an obligation not to manufacture puzzle objects so small that they might be swallowed by small children or animals.
The 'electrical' networks from which 'nice' dissections are derived may also have practical uses. As all element sizes are relatively large, so are the flows in the graph edges. This may assist in balancing network loads or may have other applications.
One measure of 'niceness' is the ratio of side of the dissection to the size of the smallest element. In a non-square rectangle the sides have different dimensions, for a very elongated rectangle it would be better to pick the shorter side as the dissection side in the ratio, picking the long side in this case would attentuate the ratio too much and skew the measure. If the sides are nearly the same length, or the rectangle is square, it doesnt matter which side is picked, so we should always pick the shorter side in rectangles. Another measure of 'niceness' is the ratio of size of the largest element to the size of the smallest element. This is what I prefer to use, dissections which are 'nice' have good measures using either method. Squared rectangles (non-square ones) are much 'nicer' than squared squares. In order 23 I found a SPSR 7526x5620 with largest/smallest elements of 2182 and 576; a ratio of 2182/576 = 3.788. This was the only one with a ratio below 4, out of a collection of 291 million SPSRs but there were many with a ratio of 4 and above. The collection of squared squares is smaller, and the best found so far is an SPSS in order 36 with a side of 7743, and largest/smallest elements of 2456 and 333; a ratio of 2456/333 = 7.38, double that of the 'nicest' SPSR, though there was a larger 'pool' to draw SPSRs from.
In May 2014, Jim Williams found a SPSS with a largest/smallest element of 549/70 = 7.8429, making this the 'nicest' known perfect squared square at the time.
Since then, Jim Williams has continued the computer search for complete orders of Perfect Squared Squares. He has enumerated all SPSSs up to order 37 and all CPSSs up to order 39. Among the SPSSs are 4 new record breaking 'nice SPSSs, with ratios of 7.38, 7.43, 7.43 and 7.56. The CPSSs have been completely enumerated up to order 39, but only 2 CPSSs exist with a 'niceness' measure below 10.

These 4 PSS have a 'niceness' measure below 8, including the SPSS with the best ratio (7.38) of largest element (2456) to smallest element (333).
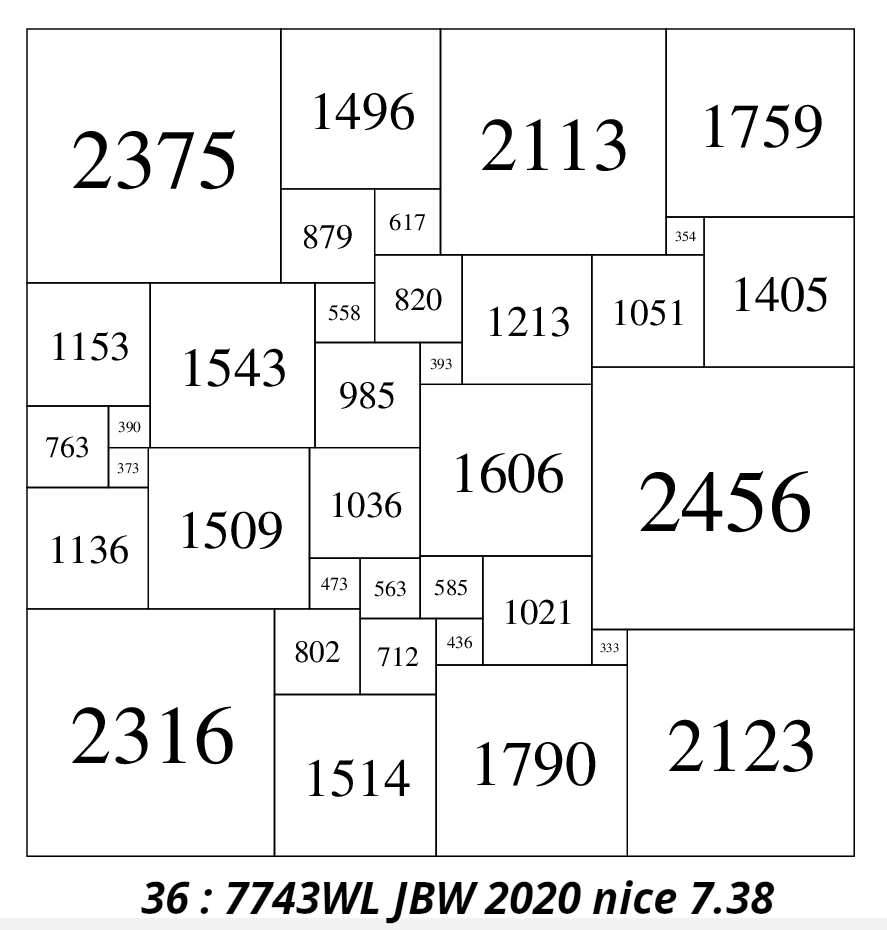
Enlargement of the 'nicest' known SPSS in 2020 with a ratio of largest element to smallest element of 2456/333 = 7.38
In 2020 I have collected together 99 of the'nicest' known PSSs - all with a niceness measure less than 10, including 97 SPSSs and 2 CPSSs.
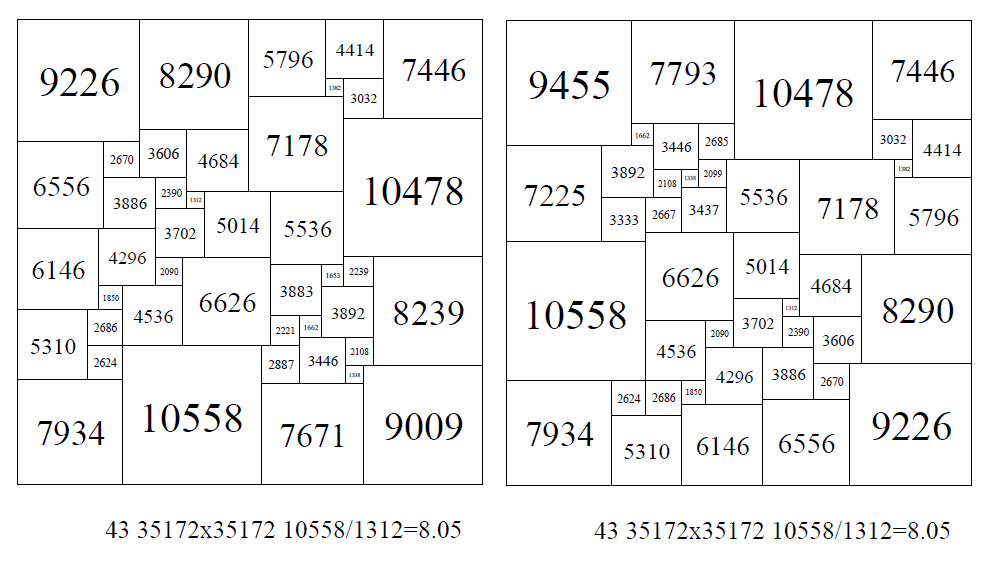
2 SPSSs of the same size, with many elements the same and with the same ratio of largest element to smallest element of 10558/1312 = 8.05
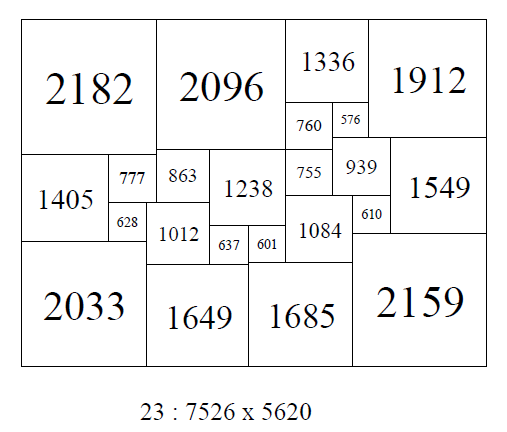
The nicest SPSR known; order 23 SPSR; 7526 x 5620 with ratio of largest element to smallest element of 2182/576 = 3.79
Maximum Number of Largest Elements Not On the Boundary (and Not in Corners)
The largest square can be on the external wall of the dissection or in the interior. Duijvestijn found two lowest order SPSRs with the largest corner not on the boundary in order 17 in 1980 [9]. He also found the lowest order SISS with this property in order 21 (see here). In 1992 Duijvestijn found the 2 lowest order SPSSs (o25:506A and o25:556A) with the largest corner not on the boundary in order 25, (see here).
SPSS o25:506 (AJD) shows it is possible for all 4 largest elements not to be in corners. SPSS o32:456A (JBW) 2013, shows it is also possible for all 5 of the largest elements not to be in corners, and o32:1376A (JBW) shows it is possible for all 7 of the largest elements not to be in corners (but the largest square is on the boundary). Among SPSS orders 21 to 32, the number of SPSSs with the largest element(s) not on the boundary are; 0, 0, 0, 0, 2, 0, 1, 6, 3, 22, 35, 120. Among CPSS orders 24 to 32, the number of CPSS isomers with the largest square not on the boundary are; 0, 0, 0, 0, 0, 0, 0, 24, 41.
SPSSs, orders 25 to 32, with the largest element not on the boundary are here. CPSS isomers, orders 31 to 32, with the largest element not on the boundary are here.
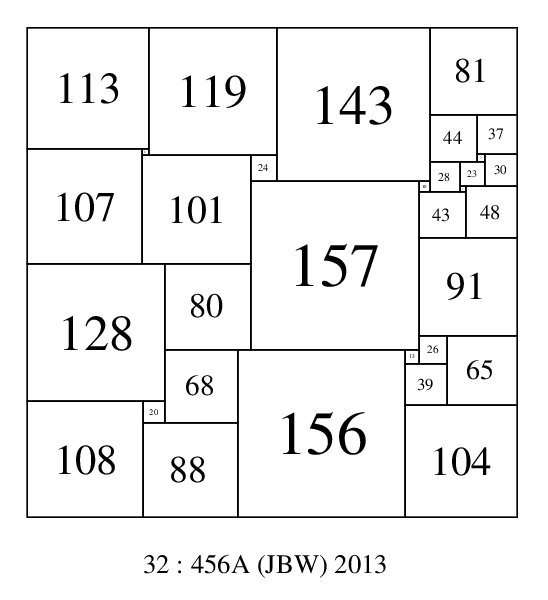
SPSS with the largest element not on the boundary and the 5 largest elements not in a corner; 32-456A-(JBW)
Minimum Number of Boundary Elements in a PSS (7)
It is not difficult to prove that there must be at least 7 elements on the boundary of a PSS. For a start, there need to be at least 4, one for each corner. If there were only 4, and they cant overlap, they would all have to be the same size, and hence imperfect. A 5 element perimeter in a squared square is not possible without both gaps and imperfection. It can also be shown with elementary algebra and examination of the various cases that 6 elements on the perimeter results in imperfect elements. The first PSS with 7 boundary elements occurs in order 28 and is a SPSS. It was found by Jasper Skinner and the Bowkampcode is 28 831 831 (423,408)(131,102,175)(117,60,63,67,116)(57,3)(54,12)(8,26,33)(20)(29,73)(2,24)(22)(17,16)(292)(291)(248) * 28 : 831C JDS. The next appearance of a 7 element boundary PSS is in order 29 SPSSs; 29 1113 1113 (569,544)(173,136,235)(161,78,73,52,57,148)(21,22,9)(4,53)(13)(5,88,1)(36)(83)(51,38)(37,99)(396)(383)(334) * 29 : 1113B AJP 2011. This was found by Anderson, Johnson and Pegg in 2011. In order 30 SPSSs there are 11, in order 31 SPSSs there are 46, in order 32 SPSSs there are 121. A pdf of the SPSSs with a boundary of 7 in orders 28-32 are here.
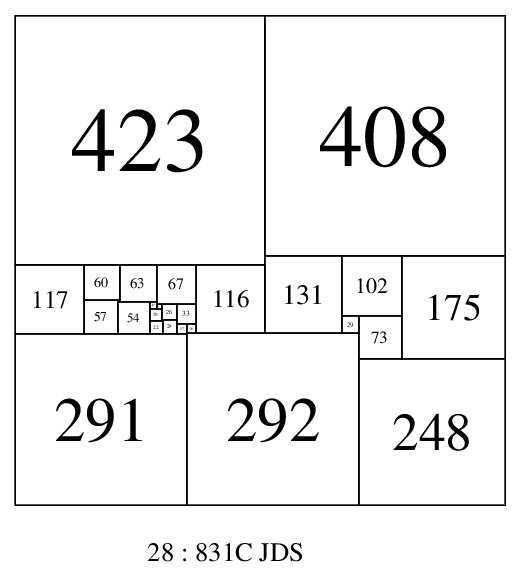
7 element boundary SPSS; 28:831C (JDS)
CPSSs with 7 elements on the boundary start in order 30. There are 4 CPSS isomers in order 30, 28 CPSS isomers in order 31 and 60 CPSS isomers in order 32, all with 7 element boundaries. A pdf showing them is here.
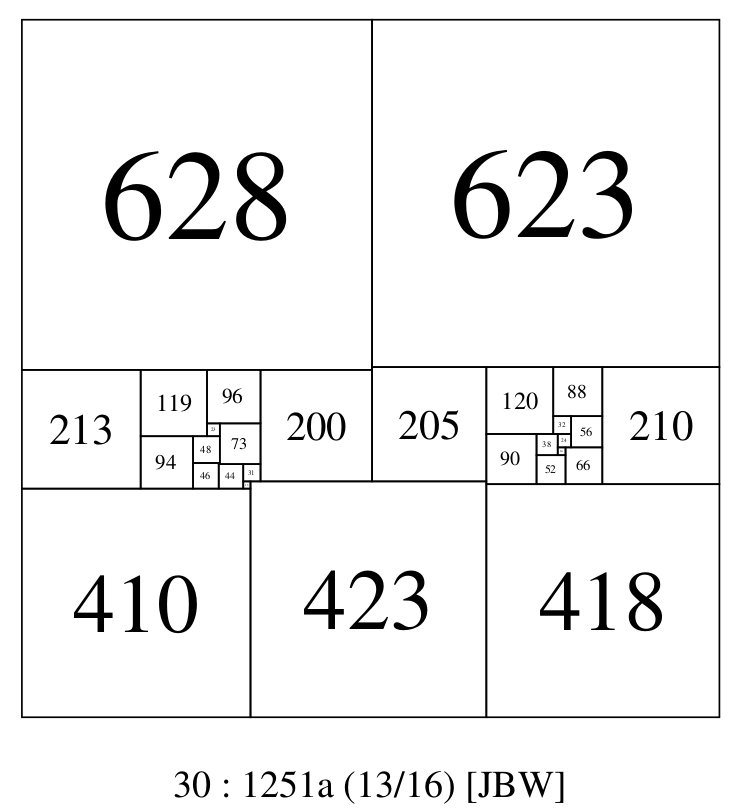
7 element boundary CPSS; 30:1251a (JBW)
Maximum Number of Boundary Elements in a PSS (>50%)
This entry is the opposite of the last, instead of trying to minimize the number of boundary elements, we are trying to maximize them. For PSS, as at least 7 squares must be on the boundary, the number of interior squares is <= order - 7. The absolute minimum number of interior squares known for SPSS is 11 in order 22. Generally for SPSS, the number of interior elements outnumbers the number of boundary elements, but in orders 25, 27, 28, 29, 31, 33, 34 and 39 the opposite occurs in some rare cases. For CPSSs there are examples where boundary elements also outnumber interior elements, and the frequency of this occurance is higher than with SPSSs. There are CPSS isomers known with this property in all orders from 25 to 32. The best result known in CPSS isomers is 31:1155b (86/256) with 18 boundary elements and 13 interior elements. This PSS also has a 9 element in the top left corner, it is shown below.
A file of SPSSs where interior elements outnumber boundary elements is here.
A file of CPSS isomers where interior elements outnumber boundary elements is here.
CPSS.png)
boundary elements = 18, interior elements = 13, & 9 in corner CPSS; 31-1155b-86-of-256-(JBW)
Minimum Size (5) of Boundary Element in a PSS
In Gambini's thesis, he proved that the smallest possible element on the boundary of a SPSR is 5. This can be extended to SPSSs and CPSSs. Gambini used this bound to improve the efficiency of his decomposition program and was able to produce 2 examples in order 44 and order 58 of SPSSs with a 5 on the side of each. He did not produce any SPSRs with 5 on the side. In September 2011 Brian Trial found 3 SPSRs of order 28 with '5 on the side'. The dimensions of the 3 SPSRs are; 658x506, 749x611 and 1226x979. A pdf with all 3 tilings is here. The lowest order SPSR with a '5 on the side' is not known, it exists somewhere between the lower bound of order 25, established by Stuart Anderson's search of order 9 - 24 and the upper bound of order 28, established by Brian Trial.
The smallest squares on the boundary in SPSR orders 9 to 24 are recorded as OEIS Integer Sequence A195984 and also in the following table;
The Smallest Boundary Squares in Each SPSR Order Order
(SPSRs)Min boundary element 9
8
10
13
11
22
12
18
13
14
14
13
15
11
16
9
17
6
18
9
19
7
20
7
21
8
22
6
23
8
24
7
The bouwkampcodes of the 3 order 28 SPSRs found by Brian Trial;
28 659 506 (357,302)(98,204)(149,87,78,43)(35,106)(9,33,71)(62,34)(10,23)(28,16)(8,15)(12,4)(3,1)(2,7)(5)
28 749 611 (387,362)(25,88,249)(224,125,63)(62,89)(99,61,27)(44,72)(38,23)(16,28)(15,8)(4,12)(1,3)(7,2)(5)
28 1226 979 (647,579)(179,400)(332,204,111)(69,221)(24,45)(128,79,21)(66)(49,30)(25,41)(19,11)(9,16)(8,3)(2,7)(5)
Minimum Corner Element Size in a PSS
In Gambini's thesis, he proved that the smallest possible corner element of a SPSR is 9. He used this as a bound in his programs to speed up the search for PSSs. Examination of SPSRs of the completed orders from 9 to order 24, shows that the order 9 33x32 SPSR (discovered by Moroń in 1925) is the only known SPSR with elements 9 and 14 in corners. Indeed no SPSRs exist in orders 9 to 24 with corners of 10, 11, 12 or 13. It is conjectured that corners of 9 and 14 can only appear in the order 9 33x32 SPSR and in no other SPSR. Gambini conjectured 33x32 would appear in the corner of a CPSS as a subrectangle, allowing 9 to be the smallest corner element of a PSS. Indeed such a CPSS has been found, see the 31:1155b (86/256) found by James Williams in Jan 2013, under the heading Maximum Number of Boundary Elements in a PSS (>50%) on this page.
The smallest known absolute corner size for an SPSS is found in the two order 22 SPSS of size 110 (110 is the smallest possible size for a SPSS). Both have a square of size 18 in a corner.
On 3rd November 2011, Brian Trial has found a 713 x 661 order 51 SPSR with 11 in the corner!. This means it may be possible to form a CPSS with 51: 713x661 as a subrectangle with 11 in a corner. No size 10 has been found in a corner in a SPSR. We do not know if PSSs with corner sizes between 10 and 18 exist, so we look to SPSR as a guide to what might be possible. The smallest corner square in each SPSR order from order 9 to order 24 is 9, 15, 25, 22, 24, 23, 23, 17, 15, 17, 16, 16, 17, 18, 16, 15. No SPSRs are known with corners of 10, 12 or 13.
One can also examine corner sizes in PSSs measured relative to the size of the PSS, for example 27:876C (JDS) has an element size 50 in a corner which is a ratio of 876/50 = 17.52, which is greater than 110/18 = 6.1, so the 27:876C 50 corner is much smaller than the 22:110A&B 18 corner, relatively speaking.
The Maximum and Minimum Number of Prime Elements in a PSS (by Order), and the distribution of Prime Elements in PSSs.
What are the maximum and minimum numbers of prime elements in a PSS. Of course the maximum number will probably increase without bound as the order increases, so a more interesting question is what is the maximum and minimum numbers of prime elements in a PSS as a proportion of the order? An even more interesting question is how are prime elements distributed in PSSs?.
After testing each and every element in all orders from order 21 to order 32 for SPSSs we obtain the following counts of primes in each SPSS which are entered in the table.
SPSS Total SPSS in each order with the number of prime elements by columns Order Order 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Total SPSS
21 0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
22 0
0
0
0
0
1
1
1
3
2
0
0
0
0
0
0
0
0
0
8
23 0
0
0
0
0
3
4
1
2
1
1
0
0
0
0
0
0
0
0
12
24 0
1
0
1
4
5
5
5
2
2
0
1
0
0
0
0
0
0
0
26
25 0
5
0
8
20
29
26
23
18
19
6
5
1
0
0
0
0
0
0
160
26 0
3
14
23
43
55
68
81
68
49
22
10
4
1
0
0
0
0
0
441
27 1
9
28
66
101
173
183
181
171
123
68
32
15
1
0
0
0
0
0
1152
28 9
26
81
175
340
439
517
464
369
292
177
81
23
6
2
0
0
0
0
3001
29 27
77
239
494
875
1150
1275
1207
1058
761
430
200
84
18
4
2
0
0
0
7901
30 74
219
716
1528
2415
3083
3259
3157
2450
1756
1060
545
216
66
19
3
0
0
0
20566
31 235
647
2083
4272
6584
8056
8582
7914
6379
4667
2789
1402
612
233
61
19
6
0
0
54541
32 814
2018
5997
12068
17515
20987
22289
20652
16516
11689
7290
3731
1678
650
209
43
12
2
1
144161
The experimental evidence suggests prime elements in SPSSs have a normal distribution with mean and variance 'approximately' equal to Order/4. It appears to be positively skewed. Above order 26 the mode seems to be fixed on 6 prime elements per SPSS.
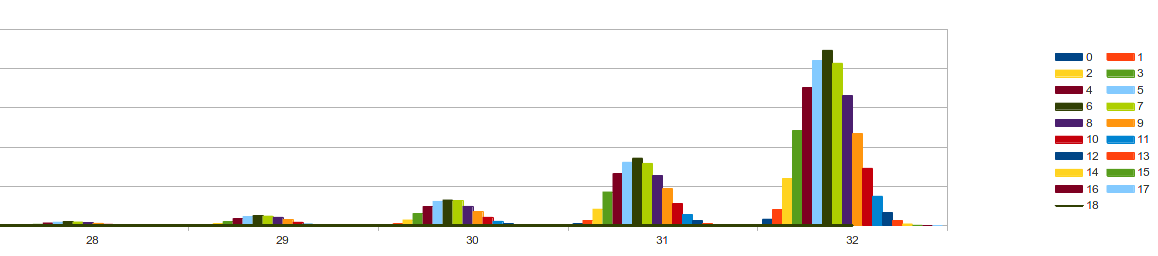
Distribution of primes in SPSS Orders 28-32
The table and histograms suggest that as the order increases, more SPSSs should be found with the number of prime elements at a maximum around order/2, and increasing to greater than order/2. In fact it is a little higher than order/2. As the table shows there is 1 SPSS of order 26 with 13 (50%) elements prime, in order 28 there are 2 SPSSs with 14 (50%) elements, in order 29 there are 2 SPSSs with 15 (51.7%) prime elements, in order 30 there are 2 SPSSs with 15 (50%) prime elements, in order 31 there are 6 SPSSs with 16 (51.7%) prime elements, and in order 32 there are 12 SPSSs with 16 (50%) prime elements, 2 SPSSs with 17 (53%) prime elements and 1 SPSS with 18 (56%) prime elements.
As the order increases the prime element minimum, ie number of PSS with no primes, increases more rapidly than the maximum. The number of SPSSs with 0 prime elements from orders 21 to 32 is; 0, 0, 0, 0, 0, 0, 1, 9, 27, 74, 235, 814.
Further analysis has been done, which involves simulating the elements of perfect squared squares as random collections of integers of an order, constrained in number to the order and in size to the maximum element size of the given perfect squared square order. The random elements are squared, then summed, and where the sum of all squares is itself a square, one finds the random integers have the same distribution of primes as do perfect squared squares. This is despite the fact that the random integers in every case did not tile the larger summed square. The requirement that PSS squared elements and the simulated random squared elements sum to a square, skews the distribution the same way in both cases. The prime composition of squared squares does not appear to be affected by the topological property of tiling.
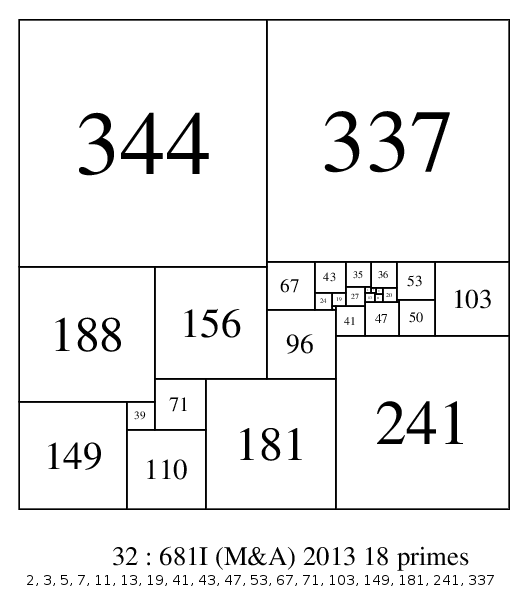
32:681I with 18 prime elements (56.25%)
Element Parity Counts in PSSs
If a count is made of the number of odd elements and the number of even elements in PSSs, it quickly becomes obvious that the parity totals of PSS elements are not equal, with a difference of several percentage points in some orders. Odd elements outnumber even elements in SPSS orders 21, 24, 25, 26 and 27, but the reverse is true in orders 22, 23, 28, 29, 30, 31 and 32. Also if we count the number of SPSSs with odd and even sides in each order, once we get past the lower orders up to 25, we find that even sides outnumber odd sides, and the split seems to converge to a 60/40 % split.
Joe DeVincentis, as far as I am aware was the first to make an observation regarding parity in square packing that provides a theoretical explanation for the parity biases of elements that we find in PSS orders, from mathpuzzle.com;
" I expressed this concept to Erich Friedman while working on a square-packing problem of his some time ago (fewest integer-sided squares to fill a given square). I noticed that many of my best solutions for odd-sided squares (which was all of them, because composite-sided squares could invariably be done best as a blown-up version of the solution for their smallest factor) had exactly 5 odd-sided squares, and this was the minimum number of such squares by a parity argument. The area of a square of odd integer side is congruent to 1 mod 4, and the area of an even square is congruent to 0 mod 4. Thus, to fill this square, you need a number of odd squares that is 1 mod 4, and the smallest value, 1, could only be done using the degenerate solution of filling the square with a square, because of the parity issue in every row and column. The next smallest possible value was 5, and many of my solutions exhibited this, with an arrangement of odd squares that consisted of one large odd square in each of two opposite corners, and 3 smaller squares that formed an L-shaped path between those two, arranged so that each column and each row contained either 1 or 3 odd squares."
Joe DeVincentis was solving one of Erich Friedman's square-packing problems where the restriction to 'perfect' tilings do not apply. As a result he was able to find solutions for odd-sided squares with 5 odd squares. The data for PSSs suggests the minimum number of odd elements in a odd-sided square is 9, a number that is also congruent to 1 mod 4. Indeed all PSSs obey this rule; they all have the number of odd elements in an odd-sided square equal to a number which is congruent to 1 mod 4, ie 9, 13, 17, 21, etc. Joe DeVincentis also makes mention of the parity constraints on an even-sided square dissection, "the area of an even square is congruent to 0 mod 4". Joe DeVincentis's observations combined with some reasoning on the definitions and properties of squared squares gives a reasonably complete explanation. The elements of squared squares are always divided by any common factors among the elements so that the GCD of the elements is 1. They are then called reduced elements. It follows that the reduced elements cannot all have a common factor of 2, ie they cannot all be even elements. What about odds? Is it possible for a PSS to consist of all odd elements? No. In the Brooks, Smith, Tutte and Stone paper (The dissection of rectangles into squares [1940]), p237 (6.22) it states, "For the reduced elements, we can prove (using the Euler polyhedron formula, and some consideration of the various cases) (6.22) At least three of the reduced elements of any perfect rectangle are even. (Three is the best number possible)." The proof is not given in the paper but appears in Skinner's book 'Squared Squares, Who's Who and What's What' p149-150, in a revised form; In a non-trivial perfectly squared rectangle, at least 2 elements are even. In the later proof the even element bound has been revised down from 3 to 2, however in either case it is true that not all the elements can be odd. So squared rectangles (of which squared squares are a special case) must contain both odd and even reduced elements. Now applying Joe DeVincentis's parity observation to an even-sided PSS, the area of a square of odd integer sided element is congruent to 1 mod 4, and the area of an even square element and an even-sided PSS is congruent to 0 mod 4. Thus, to fill the even-sided PSS, you need a number of odd squares that is congruent to 0 mod 4, and the smallest value, 4, does not appear in PSS, most likely due to the need to avoid 'imperfection' and the constraining need for parity addition of elements horizontally and vertically. The next smallest possible value is 8. This is precisely the smallest number of odd elements that appears in even-sided PSSs in all orders from 22 onwards.
As the PSS order increases, the number of possible mod 4 parity classes for both odd and even sided PSSs grows larger. The number of odd-sided elements in an odd-sided PSS is always congruent to 1 mod 4, and the number of even-sided elements in an odd-sided PSS is the order minus the odd elements. Similarly the number of odd-sided elements in an even-sided PSS is always congruent to 0 mod 4, and again the number of even sided elements in an even-sided PSS is the order minus the odd elements.
Parity in SPSSs Odd side SPSSs Even side SPSSs SPSS total for order Total odd side SPSSs by order & mod 4 class Odd element mod 4 class count
Even element mod 4 class count
Total even side SPSSs by order & mod 4 class
Odd element mod 4 class count
Even element mod 4 class count
Order 21 4k+1
4k
Order 21
4k
4k+1
0 13
8
1
12
9
0
1
1
Order 22 4k+1
4k+1
Order 22
4k
4k+2
1 9
13
2
8
14
2 13
9
3
12
10
3
5
8
Order 23 4k+1
4k+2
Order 23
4k
4k+3
3 9
14
1
8
15
1 13
10
7
12
11
4
8
12
Order 24 4k+1
4k+3
Order 24
4k
4k
8 9
15
1
8
16
5 13
11
12
12
12
13
13
26
Order 25 4k+1
4k
Order 25
4k
4k+1
21 9
16
13
8
17
24 13
12
43
12
13
16 17
8
43
16
9
61
99
160
Order 26 4k+1
4k+1
Order 26
4k
4k+2
46 9
17
24
8
18
49 13
13
114
12
14
56 17
9
150
16
10
0 21
5
2
20
6
151
290
441
Order 27 4k+1
4k+2
Order 27
4k
4k+3
117 9
18
58
8
19
184 13
14
269
12
15
178 17
10
341
16
11
0 21
6
5
20
7
479
673
1152
Order 28 4k+1 4k+3
Order 28
4k
4k
275 9
19
170
8
20
486 13
15
644
12
16
497 17
11
850
16
12
4 21
7
75
20
8
1262
1739
3001
Order 29 4k+1
4k
Order 29
4k
4k+1
523 9
20
462
8
21
1086 13
16
1677
12
17
1540 17
12
2235
16
13
38 21
8
340
20
9
3187
4714
7901
Order 30 4k+1
4k+1
Order 30
4k
4k+2
1347 9
21
1202
8
22
2791 13
17
4426
12
18
3891 17
13
5221
16
14
296 21
9
1392
20
10
8325
12241
20566
Order 31 4k+1
4k+2
Order 31
4k
4k+3
3107 9
22
3172
8
23
6844 13
18
11122
12
19
10028 17
14
13067
16
15
1600 21
10
5589
20
11
0 25
6
12
24
7
21579
32962
54541
Order 32 4k+1
4k+3
Order 32
4k
4k
7831 9
23
8832
8
24
16844 13
19
27191
12
20
24877 17
15
33333
16
16
7089 21
11
18013
20
12
7 25
7
144
24
8
56648
87513
144161
Order 33 4k+1
4k
Order 33
4k
4k+1
19309 9
24
22737
8
25
40519 13
20
68113
12
21
61075 17
16
83417
16
17
26905 21
12
54799
20
13
101 25
8
1222
24
9
147909
230288
378197
Order 34 4k+1
4k+1
Order 34
4k
4k+2
47575 9
25
61120
8
26
96942 13
21
173078
12
22
147808 17
17
207592
16
18
90318 21
13
155671
20
14
1241 25
9
9635
24
10
0 29
5
1
28
6
383884
607097
990981
Order 35 4k+1
4k+2
Order 35
4k
4k+3
115639 9
26
159051
8
27
232171 13
22
439563
12
23
357036 17
18
515228
16
19
276668 21
14
415722
20
15
9833 25
10
57163
24
11
0 29
6
7
28
7
991347
1586734
2578081
Order 36 4k+1
4k+3
Order 36
4k
4k
283471 9
27
414954
8
28
559581 13
23
1108413
12
24
863056 17
19
1272590
16
20
778961 21
15
1059018
20
16
62414 25
11
271436
24
12
6 29
7
167
28
8
2547489
4126578
6674067
Order 37 4k+1
4k
Order 37
4k
4k+1
686895 9
28
1065100
8
29
1330637 13
24
2764305
12
25
2069841 17
20
3122351
16
21
2052952 21
16
2605536
20
17
318293 25
12
1068099
24
13
145 29
8
2764
28
9
6458763
10628155
17086918
The number of even elements in a PSS is dependent on the number of odd elements and is affected by the mod 4 congruence of both the size of PSS and the order. A study of the above table reveals some rare PSSs with small numbers of even elements. In particular up to order 37 there are only 3 even-sided SPSSs (2 of order 26, and 1 of order 34) with a minimum of 6 even elements and only 41 SPSSs with a minimum of 7 even elements. A pdf which includes the 3 SPSSs with 6 evens is here.
These results are consistent with the theorem in Skinner's book (provided by Arthur Stone), but leave some unanswered questions. Was the theorem in Skinner's book meant to replace the one alluded to in 1940? What is the smallest number of even elements that can appear in a PSS? Is it 6 for squared squares, or can we get it down to 3 (or 2) like for squared rectangles? The requirement for parity addition horizontally and vertically across the dissection would make a minimum of 2 even elements in a squared square difficult if not impossible. Both versions of the theorem refer only to perfect squared rectangles, which include perfect squared squares as a special case. DeVincentis's observation applies the same way to perfect squared rectangles where both sides are even (the area is congruent to 0 mod 4, so the number of odd elements in the dissection must be also), and it applies with some modifications to perfect squared rectangles with sides which are both odd (the area is congruent to 1 mod 2) and to perfect squared rectangles with sides which are both even and odd (the area is congruent to 0 mod 2). So we would expect the number of odd elements in perfect squared rectangles with both sides even, to be congruent to 0 mod 4, this is the case. We would expect the number of odd elements in perfect squared rectangles with sides odd and even, to be congruent to 0 mod 2, this is the case. Finally we would expect the number of odd elements in perfect squared rectangles with both sides odd, to be congruent to 1 mod 2, this is also the case. In all these cases the theory based on the Brooks, Smith, Tutte, Stone 1940 result, the new theory derived from DeVincentis's observation, and computer analysis of the perfect squared rectangle catalogues are all in agreement. In perfect squared rectangles the catalogues show that the lowest number of odd elements in a dissection is 4 and the smallest number of even elements is 3. The first SPSR with 3 even elements appears in order 10, but an even element count of 3 is rare in SPSR orders.
Element Situated at the Center of a PSS
The requirement for all elements of perfect squared squares to be different sizes, (i.e. 'perfection'), scatters the elements within the dissection, and eliminates all symmetry in the composition. However it may be possible for an element to be situated at the exact center of a PSS. This is the case with squared windmills, which are compound. Such things do occur in SPSSs, but are quite rare. Only 1 exists in the SPSS orders from 21 to 32, 28:888A(JDS) and only 7 others have been found in SPSS orders up to 43. Thanks to Geoffrey Morley for locating all of those. Here they are in a pdf.. And here are their central squares and Bouwkampcodes;
76 in 28 888 888 (340,222,326)(118,104)(14,70,119,227)(181,225,66)(10,60)(76)(11,108)(26,45)(83,19)(64)(137,44)(335)(93,323)(230)
!!! Update !!! Bernard Moss has used a transform to produce millions of SPSSs with a central element in orders 48 to 85!
110 in 33 1210 1210 (450,357,403)(193,164)(179,224)(335,115)(29,41,94)(15,85,110,12)(53)(130)(33,101,45)(180)(56,213)(60,25)(135)(157)(90,100)(425)(415)(370)
39 in 38 977 977 (369,258,350)(111,147)(71,279)(319,125,36)(64,103,16)(87)(25,39)(136,14)(122,121)(1,51,348)(58,151,50)(101)(289,88)(57,22,9)(4,52,196)(13)(35)(144)
4 in 40 1916 1916 (736,479,701)(257,222)(35,323,565)(656,224,148)(76,72)(4,68)(304)(240,151)(60,91)(29,31)(260,313)(233,178,276)(524,132)(80,98)(78,130,25)(392)(105)(374)(339,52)(287)
20 in 41 520 520 (200,130,190)(70,60)(80,170)(142,46,32,50)(14,18)(56,4)(52,20)(100)(40,68)(90,92)(10,160)(43,59,76)(21,22)(6,36,17)(88,2)(86,29)(28)(19,74)(57)(55)
8 in 43 1280 1280 (496,324,460)(188,136)(184,412)(265,215,16)(112,92)(20,32,40)(96,36)(24,8)(232)(60)(50,165)(156)(315)(4,408)(153,404)(47,106)(204,99,59)(34,62,69)(6,28)(105)(83,7)(76)
41 in 43 2057 2057 (773,520,764)(276,244)(285,723)(640,110,23)(87,212)(197)(171,41)(326)(123,74)(49,25)(196)(172)(349,233,112)(321,319)(265,570)(89,144)(27,62)(8,333,35)(2,325)(323)(104,305)(97)(201)
210 in 43 3340 3340 (1160,1057,1123)(103,508,380,66)(1189)(672 591)(128,252)(302,210,124)(86,290)(81,510)(92,204)(753)(394)(494)(692,212)(161,1028)(867)(419,334)(168,166)(132,173,387)(336,83)(2,255,41)(253)(214)
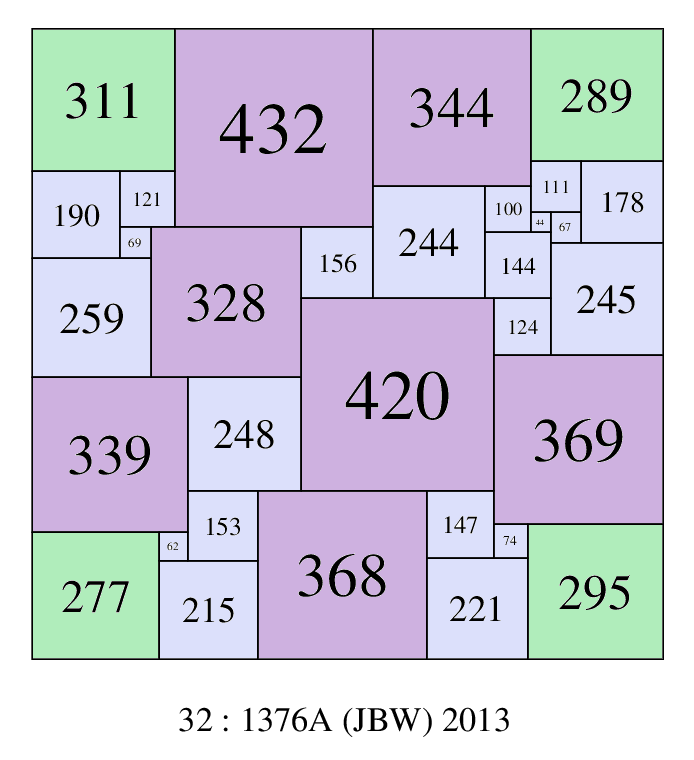
SPSS with the 7 largest elements not in a corner; 32-1376A-(JBW)
and a ratio of largest/smallest element of 432/44 = 9.81
Jim Williams has extended the complete enumeration of SPSS orders to order 37. In order 37 there is a squared square with a side of 2516 with 9 of the largest elements not in a corner.
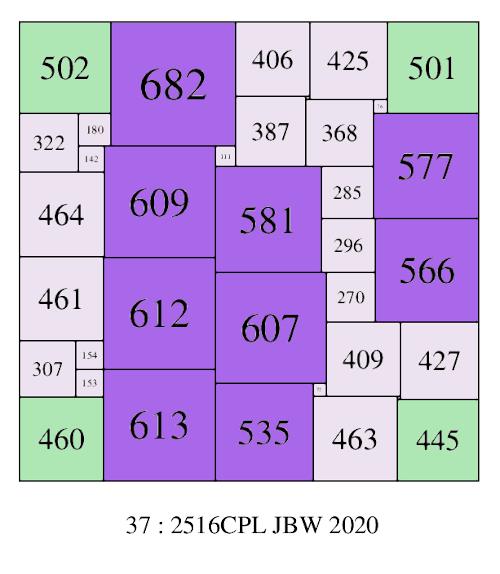
SPSS with the 9 largest elements not in a corner; 37-2516CPL-(JBW)
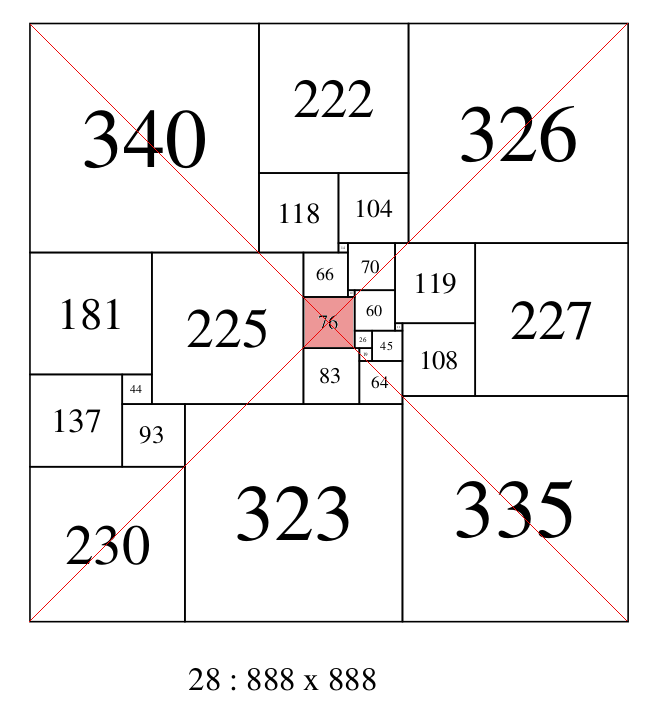
28:888A (JDS), Lowest order SPSS with a central element
References
- 'O Rozkladach Prostokatow Na Kwadraty' (On the Dissection of a Rectangle into Squares) by Zbigniew Moroń, Prezeglad Mat. Fiz. 3 152-153 (1925)
- R.L. Brooks, C.A.B. Smith, A.H. Stone and W. T. Tutte. 'The Dissection of Rectangles into Squares'. Duke Math. J. 7 (1940) 312–340.
- E401 A. H. Stone, Michael Goldberg and W. T. Tutte, The American Mathematical Monthly Vol. 47, No. 8 (Oct., 1940), pp. 570-572
- JASPER DALE SKINNER II, 'Uniquely Squared Squares of a Common Reduced Side and Order', JOURNAL OF COMBINATORIAL THEORY, Series B 54, 155-156 (1992)
- T. H. WILLCOCKS, A note on some perfect squared squares, Canad. J. Math. 3 (1951),304-308.
- W. T. Tutte, Squaring the square, Canad. J. Math. 2 (1950),197-209.
- W. T. Tutte, The Quest of the Perfect Square, The American Mathematical Monthly, Vol. 72, No. 2, Part 2: Computers and Computing (Feb., 1965), pp. 29-35
- A.J.W. Duijvestijn and P.Leeuw, Lowest Order Squared Rectangles and Squares With the Largest Element Not on the Boundary, Mathematics of Computation, Vol. 37, No. 155 (Jul., 1981), pp. 223-228