Simple Imperfect Squared Squares (SISSs) ;
Orders 13 to 32
Imperfect Squared Squares
Imperfect squared squares are more numerous (at a given order) than perfect squared squares. The counts of SISS by order are listed in the OEIS as sequence A002962 ; The number of simple imperfect squared squares of order n. Counts were obtained by processing all 3-connected planar graphs up to 30 edges as resistor networks subject to an electromotive force in each edge to obtain square tilings. All rectangles, perfect squared squares and compound imperfect squared squares have been filtered out, and any remaining duplicates eliminated, to arrive at these counts.
The number of Simple Imperfect Squared Squares (SISSs) by Order, in bouwkampcodes & pdf (orders 13 - 24 only) & postscript (orders 25 -> 31 only);
- Order 13: 1 (bkcodes) 1 K (pdf) 3.1k
- Order 14: 0
- Order 15: 3 (bkcodes) 1 K (pdf) 5 k
- Order 16: 5 (bkcodes) 1 K (pdf) 6.9 k
- Order 17: 15 (bkcodes) 1 K (pdf) 16.5 k
- Order 18: 19 (bkcodes) 1.4 K (pdf) 21 k
- Order 19: 57 (bkcodes) 4.5 K (pdf) 61 k
- Order 20: 72 (bkcodes) 6.1 K (pdf) 78 k
- Order 21: 274 (bkcodes) 16.1 K (pdf) 271 k
- Order 22: 491 (bkcodes) 34.6 K (pdf) 558 k
- Order 23: 1766 (bkcodes) 176.1 K (pdf) 2.0 M
- Order 24: 3679 (bkcodes) 387.6 K (pdf) 4.3 M
- Order 25: 11158 (bkcodes) 1.2 M (ps zipped) 394 k
- Order 26: 24086 (bkcodes) 2.8 M (ps zipped) 798 k
- Order 27: 64754 (bkcodes zipped) 1.8 M (ps zipped) 2.4 M
- Order 28: 132598 (bkcodes zipped) 4 M (ps zipped) 5.1 M
- Order 29: 326042 (bkcodes zipped) 14 M (ps zipped) 12.7 M
- Order 30: 667403 (bkcodes zipped) 27.4 M (ps zipped) 25.2 M
- Order 31: 1627218 (bkcodes zipped) 76.6 M (ps zipped) 69.5 M
- Order 32: 3508516 (bkcodes zipped) 171.5 M (ps zipped) 143 M
SISSs are by definition, imperfect, (have at least 2 squares the same size), however it is possible to get perfect squares from imperfect squares. One can 'derive' SPSSs (Simple Perfect Squared Squares) of order n-2 from SISSs of order n. This provides a means of verifying the SPSS counts obtained in lower orders.
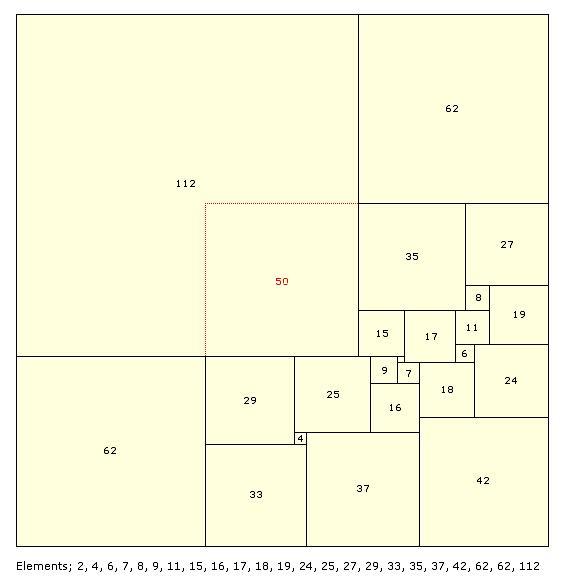
Order 23: 174 x 174 SISS with Duijvestijn's order 21 SPSS derived. The two 62 squares and the 112 square are removed and replaced with a square that is the difference of the two sizes, 112 - 62 = 50.
Imperfection can result in symmetry
As a result of squares in the tiling being the same size, some of
these 'imperfect' tilings have interesting symmetrical arrangements.
There are dissections which invariant under a 90 degree rotation, 180
degree rotation, reflection about a diagonal and reflection about
centre axes. A collection of symmetrical SISSs is here!
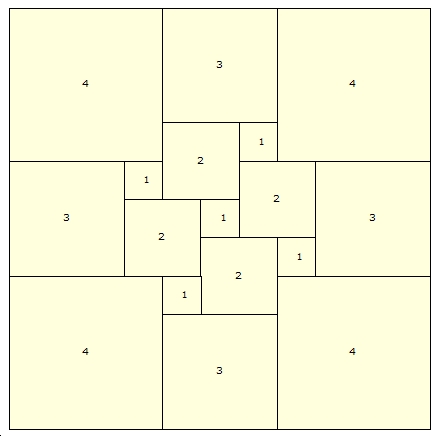
SISS (Simple Imperfect Squared Square), Order 17: 11 x 11, the tling is invariant under 90 degree rotations
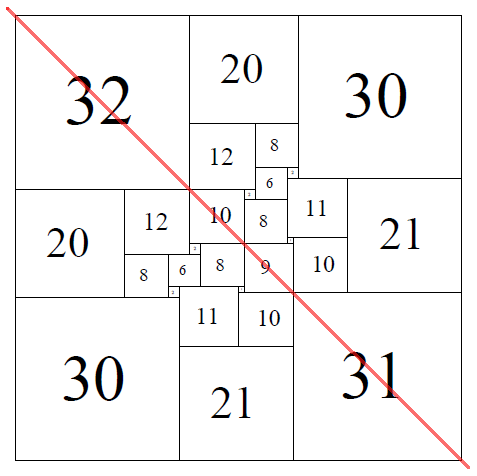
SISS (Simple Imperfect Squared Square), Order 28: 82 x 82, the tiling is symmetrical about the diagonal axis.
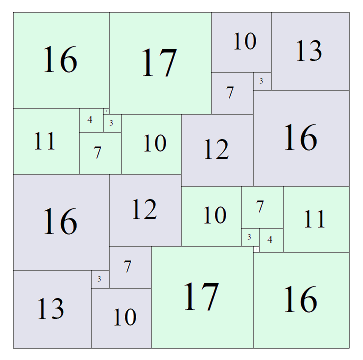
SISS (Simple Imperfect Squared Square), Order 28: 28 x 28, rotational symmetry, the tiling is invariant under 180 degree rotations
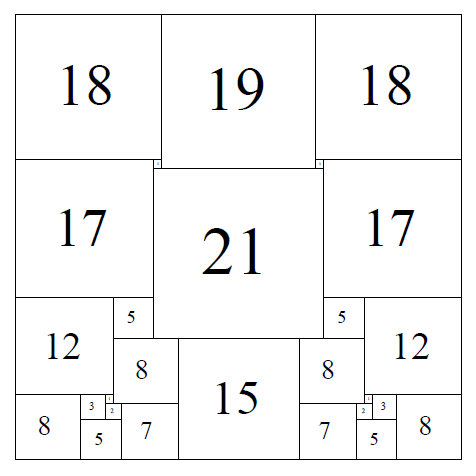
SISS (Simple Imperfect Squared Square), Order 27: 55 x 55, the tiling is symmetrical about the vertical axis