Tiling by Squares
A square or rectangle is said to be 'squared' into n squares if it is tiled into n squares of sizes s1,s2,s3,..sn. A rectangle can be squared if its sides are commensurable (in rational proportion, both being integral mutiples of the same quantity) The sizes of the squares si are shown as integers and the number of squares n is called the order.
Squared squares and squared rectangles are called simple if they do not contain a smaller squared square or rectangle, and compound if they do.
Squared squares and squared rectangles are called perfect if the squares in the tiling are all of different sizes and imperfect if they are not.
Most of the square tilings we are familiar with in our everyday lives use repeating squares of the same size, such as square floor tiles, square graph paper and the like. These repeating grid square tilings can be described using this terminology as 'imperfect' and 'compound'.
Simple and perfect square tilings are quite different in that no square of the same size is repeated. This is not so familiar, nor is it immediately obvious how to show that they exist or to be able to make them as required. In fact simple perfect squared rectangles begin at order 9 and simple perfect squared squares at order 21.
Techniques for making square tilings
Algebraic Method
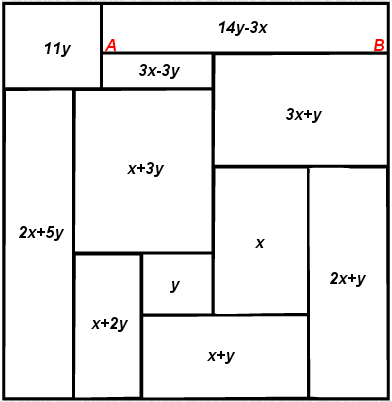
Figure 71; Algebraic Method
One method which can be done with pen and paper and some simple algebra is described by William Tutte; [1]
"The construction of perfect rectangles proved to be quite easy. The method used was as follows. First we sketch a rectangle cut up into rectangles, as in Figure 71. We then think of the diagram a bad drawing of a squared rectangle, the small rectangles being really squares, and we work out by elementary algebra what the relative sizes of the squares must be on this assumption. Thus in Figure 71 we have denoted the sides of two adjacent small squares by x and y and then that the side of the square next on the left is x+2y, and so on. Proceeding in this way we get the formulae shown in Figure 71 for the sides of the 11 small squares. These formulae make the squares fit together exactly except along one segment AB. But we can make them fit on AB too by choosing x and y to satisfy the equation (3x + y) + (3x - 3y) = (14y - 3x), that is 16y = 9x . Accordingly we put x = 16 and y = 9 . This gives the perfect rectangle of Figure 72, which is the one first found by Stone."
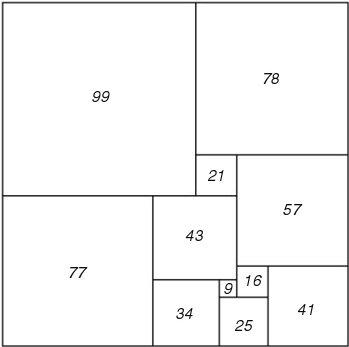
Figure 72; 177 x 176 Squared Rectangle
Creating Squared Rectangles from Electrical Networks
It was shown by Brooks, Smith, Stone and Tutte that simple squared rectangles correspond to 3-connected planar electrical networks with one edge removed and an electromotive force applied. They reinterpreted the problem as one of electrical circuits. Squares in a rectangle dissection were replaced by edges of unit resistance in an electrical network, connected as nodes at the top and bottom edges of the squares and the rectangle.
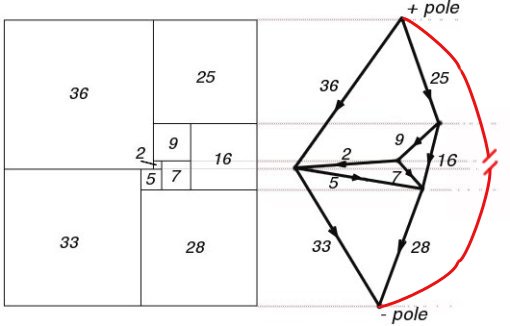
69 x 61 Squared Rectangle and its Electrical Network
By making the correspondence between electrical networks and square dissections, it becomes possible by enumerating all electrical networks with a given number of edges, to produce all possible simple tilings of rectangles with a given number of squares.
3-connected planar graphs are equivalent to the '1-skeletons' (i.e. edges and vertices) of polyhedra, this is known as Steinitz's theorem (A graph G is the edge graph of a polyhedron iff G is a simple planar graph which is 3-connected). Whitney proved 3-connected planar graphs have a unique embedding up to homeomorphisms of the non-oriented sphere, i.e. a unique planar map. This means the problem of enumerating polyhedra is the same as enumerating 3-connected planar graphs. These are also called c-nets, in Tutte's words 'The term "c-net" is sometimes used for a 3-connected map, circuits of 1 or 2 edges being excluded'. [A c-net is also used to mean a rooted 3-connected planar map, ie a 3-connected planar map with a directed distinguished edge at the outer face.] Tutte developed a theory for exhaustively creating c-nets. Tutte did this with his Wheel Theorem and also developed enumeration formulae to estimate the numbers of c-nets by edge.
Duijvestijn and Bouwkamp created c-nets by computer using this theory. The method created many duplicate c-nets so a major computational effort went into eliminating them. Recently new techniques for producing c-nets have been developed, these include Brendan MacKay and Gunnar Brinkmann's plantri which generates exactly one member of each isomorphism class for many types of planar graph, and A Direct Decomposition of 3-Connected Planar Graphs by Bodirsky, Gropl, Johanssen, and Kang.
Once a supply of c-nets has been produced, each c-net with a selected edge is treated as an electrical network. The currents and voltages in the network branches correspond to the sizes of the squares and they can be calculated using Kirchhoff's Laws and the Matrix Tree Theorem. As the simple squared rectangles are produced, they can be searched for simple perfect squared squares.
Ian Gambini's Decomposition Approach
Ian Gambini in his thesis [2] (French) has produced squared squares by two main methods using numeric decomposition algorithms, his first method for a given integer n obtains every decomposition using n squares, the second method is a lot more efficient but incomplete and allows the calculation of decompositions of a square into distinct sized squares to generate squared squares, squared cylinders and tori. Gambini has discovered over 30,000 squared squares with most in higher orders, with large sizes and mixed orientations. A selection of these are shown in his published work.
Subdivision Tiling and Squared Rectangles
Cannon, Floyd and Parry use a coded tiling file and some simple finite subdivision rules with their program subdivide.c, to recursively subdivide a tiling into a complex subdivided tiling. Another program squarect.c, inputs the tiling file and maps the boundary of the tiling onto a quadrilateral using the Riemann mapping theorem. The quadrilateral and its interior squares are calculated and output as a postscript file for the associated squared rectangle. The order of these subdivided tilings increases exponentially with the number of subdivision levels. Subdivision creates imperfect and compound tilings. The squaring of the rectangle is done using the cyclic algorithm [3]

A subdivision substitution tiling by S. Anderson using Cannon, Floyd and Parry's software subdivide and squarect.
References
- "More Mathematical Puzzles and Diversions", 1961, collection by Martin Gardner. Ch 17. 'Squaring the Square' by William T. Tutte , from 'Mathematical Games' column Nov 1958, Scientific American.
- "Quant aux carrés carrelés"; Ian Gambini, THÈSE L’UNIVERSITÉ DE LA MÉDITERRANÉE AIX-MARSEILLE II, École doctorale de Mathématiques et Informatique, Décembre 1999
- "Squaring rectangles: the finite Riemann mapping theorem", by J.W. Cannon, W.J. Floyd, and W.R. Parry, Contemporary Mathematics, Volume 169, 1994.