Tilings by Triangles
The tiles of a tiling are called its Elements. The Order is the number of elements in the tiling.
A tiling is Perfect if its elements are all of different sizes. Otherwise the tiling is Imperfect.
Tilings of the Plane by Triangles
It is well known that any triangle shape, along with copies rotated 180 degrees can tile the plane.. All quadrilaterals can also tile the plane.
Coxeter [1973] has shown that the fundamental domain of the group of symmetries in the plane generated by three mirrors can be either an equilateral triangle (angles π/3, π/3, π/3 or 60°, 60°, 60°), isosceles right triangle (angles π/4, π/4, π/2 or 45°, 45°, 90°) or half equilateral triangle (angles π/6, π/3, π/2 or 30°, 60°, 90°). Except for rectangular and square fundamental regions, the fundamental domains of all symmetries of the plane are subsets of these triangles as provided by the √2 and √3 proportional systems.
Tilings of Squares by Similar Non-Right Triangles
M. Laczkovich has shown that there are exactly three shapes of non-right triangles that tile the square with similar copies, corresponding to angles (π/8, π/4, 5π/8 or 22.5°, 45°, 112.5°), (π/4, π/3, 5π/12 or 45°, 60°, 75°), and (π/12, π/4, 2π/3 or 15°, 45°, 120°), (Stein and Szabó 1994).
Not many dissections of the square by the 3 kinds of Similar Non-Right Triangles are known. See here.
What is the smallest number of 45∘, 60∘, 75∘ triangles that a square can be divided into?
Lew Baxter has found two solutions, one with 64 triangles and one with 50 triangles and Franz Pichler found a 46 triangle solution. The 64 triangle solution is shown below, with a pdf and postscript file for download, the 50 triangle solution is a variation on the 64 triangle solution and is shown below, also with a pdf and postscript file for download.
See the Wolfram Blog entry by Ed Pegg for information on how the solutions were found, refined and proved correct.
Lew Baxter's 64 triangle solution
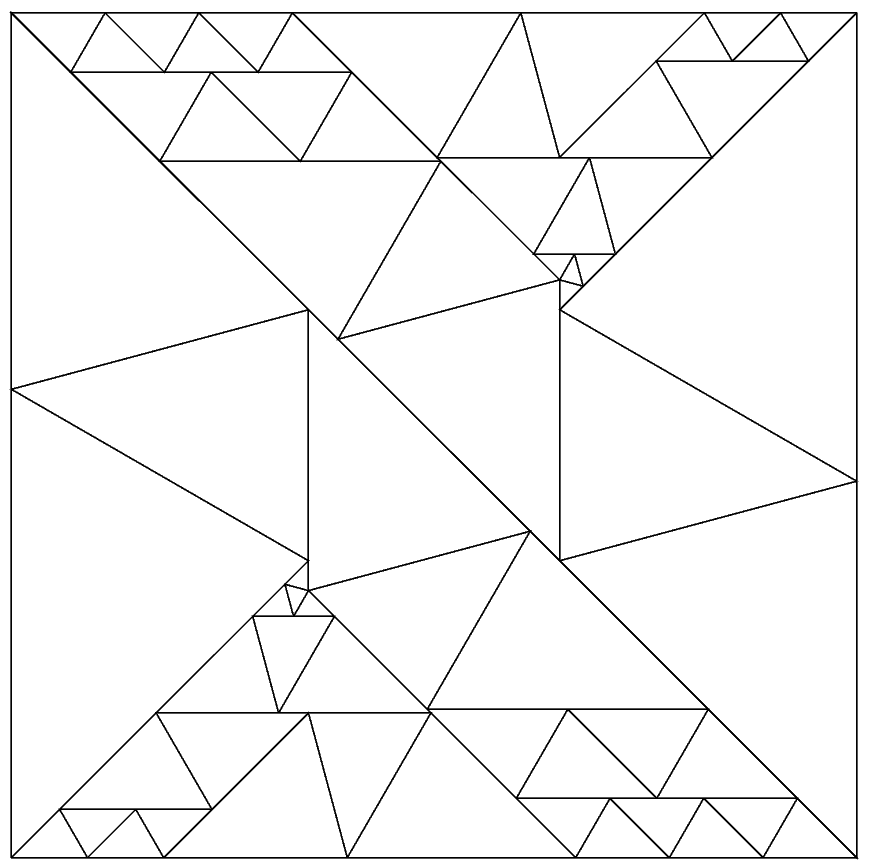
Figure 11; Lew Baxter's 64 triangle solution to dissecting a square into 45-60-75 degree triangles.
Lew Baxter's 50 triangle solution
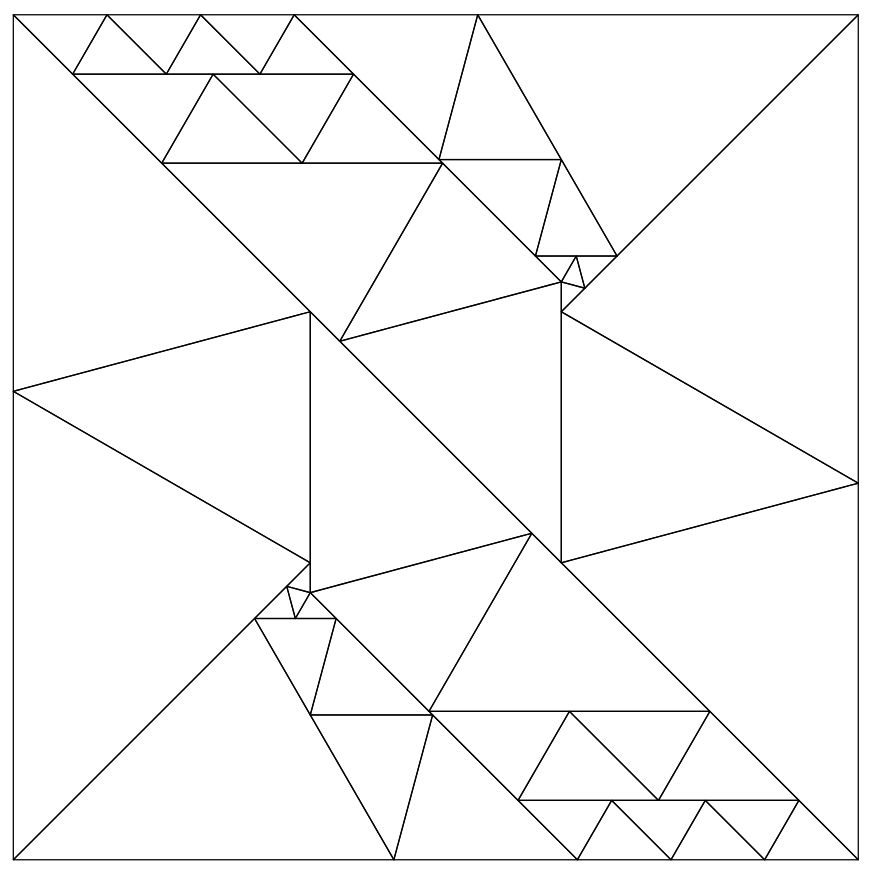
Figure 12; Lew Baxter's 50 triangle solution to dissecting a square into 45-60-75 degree triangles.
Andrzej Zak's Perfect Dissections of Equilateral Triangles
Andrzej Zak has published a paper 'A note on perfect dissections of an equilateral triangle' in 2009[13]. Andrzej notes that a perfect dissection of an equilateral triangle by equilateral triangles is not possible, but perfect dissection of an equilateral triangle into right-angle triangles is possible, and it is also possible to perfectly dissect an equilateral triangle into non-right angle triangles. He proves that 7 is the smallest number of non-right angle triangles that an equilateral triangle can be perfectly dissected into and presents an example of such a dissection.
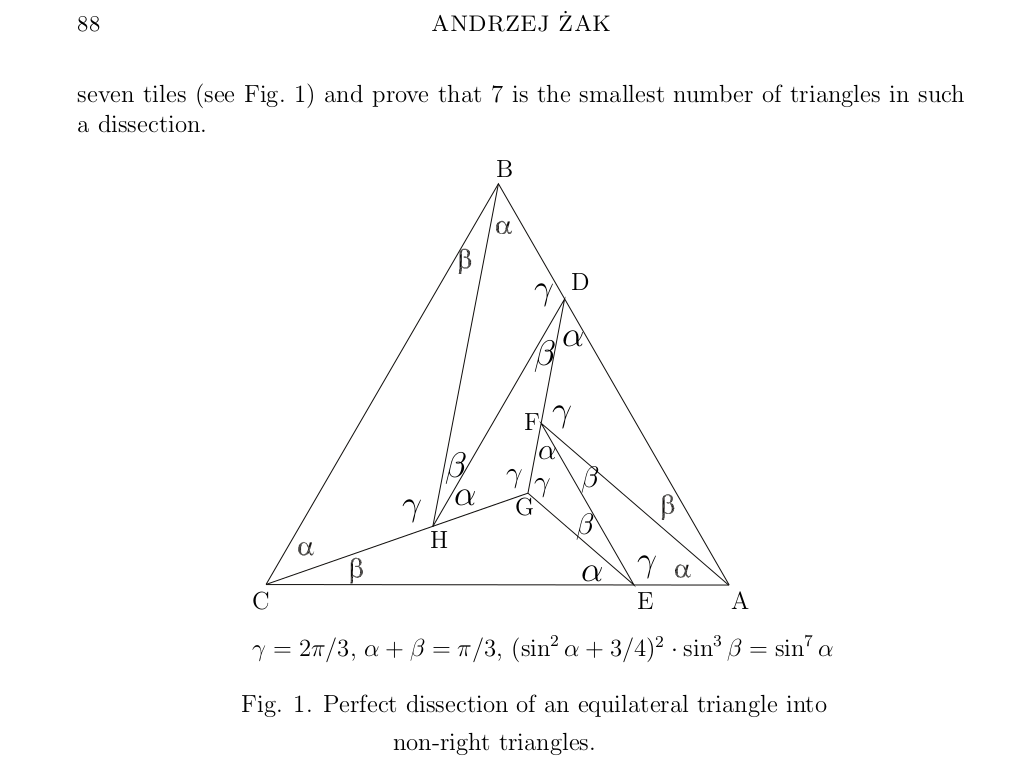
Figure 13; equilateral triangle perfect dissection into 7 non-right angle triangles.
He also gives 2 examples of a triangle (non-right angle) dissected into 5 perfect similar triangles, 5 being the smallest number possible and these 2 dissections being the only ones possible.
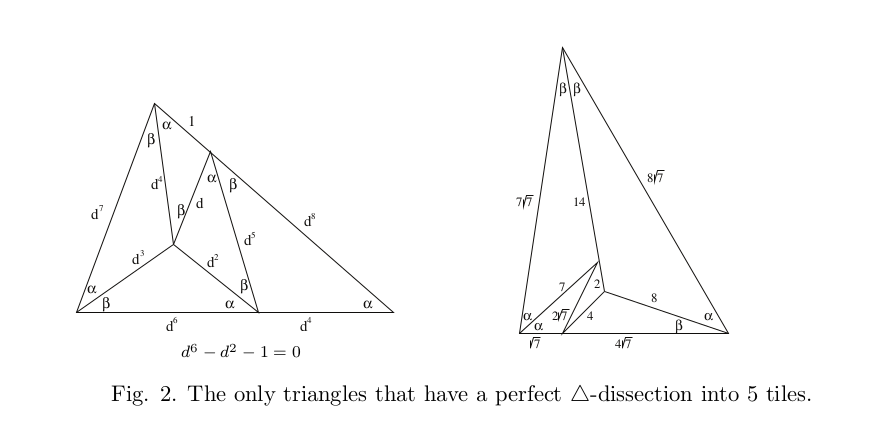
Figure 14; non-right angle triangle perfect dissections into 5 similar triangles.
Tilings of Squares by Pythagorean Triangles (Right Triangles with integer sides)
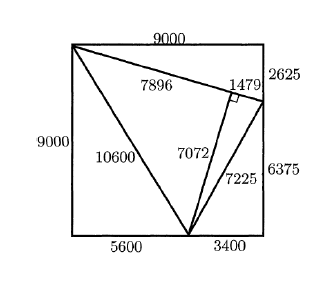
Figure 3; Jepsen & Roc's square dissected
into 5 pythagorean triangles.
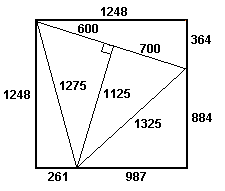
Figure 4; Penny Drastik's
square dissected into
5 pythagorean triangles.
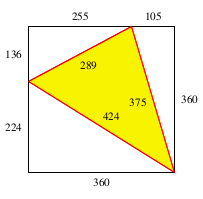
Figure 5; smallest square
dissected into 3 pythagorean
triangles and 1 non-right triangle [9].
In 'Making Squares from Pythagorean Triangles' [6] Charles Jepsen and Roc Yang show a square exists that can be dissected into m Pythagorean triangles (right triangles with integer sides) if and only if m ≥ 5. This is shown by displaying a square that can be dissected into five Pythagorean triangles, and observing that a dissection into m triangles implies a dissection of a (usually larger) square into m+ 1 squares. It then remains to be shown that no square can be dissected into 2, 3 or 4 Pythagorean triangles. The existence of such a dissection in the case m = 4 would imply the existence of a rational point (x,y) with x> 4 on a certain elliptic curve y2= x3 - 7x - 6, and algebraic geometers have shown that the curve has no such rational points. Pythagorean Theorem Extensions by Christina Lau [8], provides an explanation of Charles Jepsen and Roc Yangs work.
On the Pythagorean page of his wonderful site, Dr Ron Knott asks [11] "Is this (Figure 1) the smallest square that can be dissected into five Pythagorean triangles?
It seems this question is still "open". Can you find the answer?
Amazingly, Penny Drastik, a primary student at The Illawarra Grammar School in Australia, aged 10, found 12 smaller solutions for squares of side less than 9000 including one which she thinks is the smallest square with this pattern of triangles [April 2008].
Penny also found one square (of side less than 9000) that can be dissected in two different ways with this pattern of triangles. I leave you with the challenge of finding the sides of the triangles and the square."
Quadrillerator [10] in a yahoo answer has written a php program which confirms Penny Drastik's solution as the smallest.
Pythagorean triangles of shape 1-2-sqrt(5) with no two the same size, can tile the square. The best known solution has 8 triangles (Berlekamp 1999).[4]
Tilings by Isosceles Right Triangles and by Equilateral Triangles
The authors of "The Dissection of Rectangles into Squares" (Brooks, Smith, Stone & Tutte) extended the electrical tiling theory they developed for square dissections to the dissection of isosceles right triangles and equilateral triangles into similar triangles of different sizes.
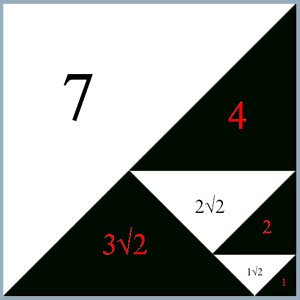
Figure 6; A.H. Stone's square dissected by isosceles
right triangles
Tilings by Isosceles Right Triangles
Isosceles right triangles of different sizes can be assembled together into larger isosceles right triangles. They can also tile other polygons such as squares and rectangles, and surfaces such as cylinders and tori.
A tiling of a polygon by isosceles right triangles is called Compound if it has a properly contained subdivided triangle or rectangle. Otherwise the tiling is Simple.
Arthur Stone dissected a square into 7 different isosceles right triangles. The size of each isosceles right triangle is represented by the length of a shorter side. This is conventionally an integer when the side is parallel to a side of the square. Jasper Skinner discovered later that isosceles right triangles can tile a square perfectly without dissecting a main diagonal. This and further discoveries led to a review of the theory by two of the original authors, C.A.B. Smith and W.T. Tutte and the publication of a joint paper {3} by all three.
Extensive catalogues of Tilings by Isosceles Right Triangles, featuring a large collection of tilings, produced and classified by Geoffrey Morley, are here.
Morley's Isosceles Right Triangulation Code. (MIRT code) is a concise notation, devised by G.H. Morley, describing a tiling by isosceles right triangles by listing the elements from top to bottom and from left to right. Each element is represented by an integer with the value 10n+d where n identifies the element's size and d its orientation. d is the direction (0-7) in which the element's right angle "points" expressed as the angle measured clockwise from the "up" direction divided by 45 degrees. The element's shorter side is n when d is odd and n√2 when d is even. The canonical orientation is determined in a similar manner to Bouwkampcode.
Option 1 (suggested by J.D. Skinner): The first element whose uppermost vertices lie on the same horizontal line segment may be prefixed by a minus sign.
Option 2: Each element may be followed by the (x,y) coordinates of the element's right-angled vertex.
The MIRT code of A.H. Stone's square depicted above is (option 1 only) -77 43 -30 24 23 -14 13, or (option 2 only) 77 0 7 43 7 3 30 3 3 24 5 1 23 7 1 14 6 0 13 7 0. In the latter case the triplets of numbers could be separated by commas.
Isomers (tilings with the same set of tiles) are ordered by their MIRT code elements (giving side length and orientation, not coordinates). The sets of isomers with the same order:side are ordered by the MIRT code elements of the first (or only) tiling in each set. For each order:side, tilings in the same set are allocated the first or next 2-letter id from a range associated with the catalogue.
Tilings by Equilateral Triangles
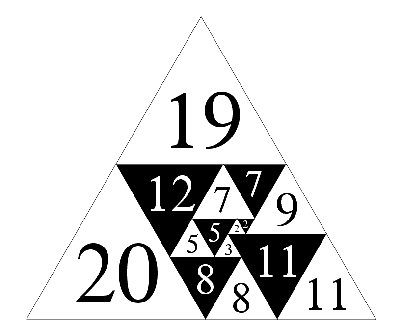
Figure 7; W.T. Tutte's equilateral triangle dissected by
equilateral triangles
The authors of "The Dissection of Rectangles into Squares" proved that an equilateral triangle cannot be dissected into equilateral triangles all of different sizes (orientation ignored). At least two triangles will be of the same size. See David Radcliffe's post for a proof. However equilateral triangles can tile in an up direction or a down direction, if these are considered different as they are not congruent, even if at the same size, then a kind of 'perfect' tiling is possible.
The equilateral triangled triangle tiling on this page by W.T. Tutte, believed by him to be the lowest order (15 elements - 2 extra polar elements = 13/2 = 6 ½) of this kind, and now proved so by Aleš Drápal and Carlo Hämäläinen[14], making it comparable to Duijvestijn's simple perfect squared square.
For more information on the theory of equilateral triangle dissections, new results in the enumeration of equilateral triangle dissections, connections to number theory and infinite dissections follow this link
Mysteries of the Equilateral Triangle
A book "Mysteries of the Equilateral Triangle" by Brian J. McCartin has recently been published on the web. It is freely available for download from www.m-hikari.com at this link.
In the preface the author describes his motivation in writing the book, and gives an overview of each of the chapters;
Chapter 1 surveys the rich history of the equilateral triangle, "We will find the equilateral triangle present within architecture, sculpture, painting, body armour, basket weaving, religious icons, alchemy, magic, national flags, games, insects, fruits and vegetables, music, television programs and, of course, Mathematics itself." Indeed many aspects of human culture embody the triangle and in particular the equilateral triangle. Perhaps the most enduring examples are in architecture. Equilateral triangles are often found in plenty of architecture, like roofs of buildings. The hotels in Cancun along the coast for instance are triangular in shape. Aesthetically, the hotels look elaborate but they are built this way because the design itself helps reinforce the structural integrity of the resorts. Something to take note of the next time you are on a Mexico vacation.

Figure 8; Gallery of equilateral triangles in buildings
(McCartin)
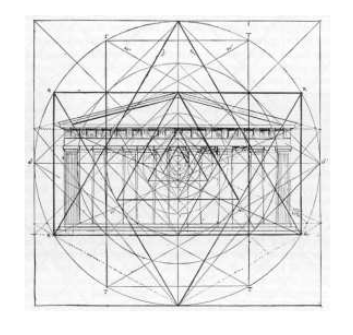
Figure 9; The Parthenon and the equilateral triangle
(McCartin)
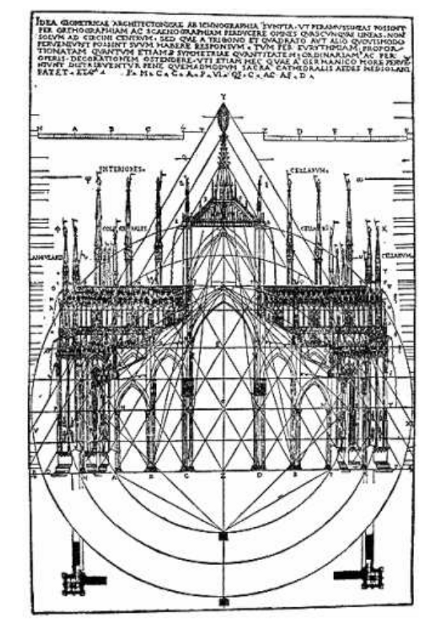
Figure 10; Milan Cathedral and equilateral triangles (McCartin)
Chapter 2 explores some of the mathematical properties of the equilateral triangle. These range from elementary topics such as construction procedures to quite advanced topics such as packing and covering problems.
In Chapter 3, the author writes, "we take up the place of the equilateral triangle in Applied Mathematics. Some of the selected applications, such as antenna design and electrocardiography, are quite conventional while others, such as drilling a square hole and wrapping chocolates, are decidedly unconventional. I have based the selection of topics upon my desire to communicate the sheer breadth of such applications. Thus, the utilization of the equilateral triangle in detecting gravitational waves, the construction of superconducting gaskets, cartography, genetics, game theory, voting theory as well as many other areas have all been included."
No book on triangles would be complete without mathematical recreations, and Chapter 4 is given over to this; "The subject of Chapter 4 is the role of the equilateral triangle in Recreational Mathematics. Traditional fare such as dissection puzzles appear on the menu, but so do more exotic delicacies such as rep-tiles and spidrons. Devotees of the work of Martin Gardner in this area will instantly recognize my considerable indebtedness to his writings. Given his extensive contributions to Recreational Mathematics, this pleasant state of affairs is simply unavoidable."
The last chapter is given over to a collection of quite difficult problems concerning the Equilateral Triangle, along with a "Gallery of Equilateral Triangles that has been appended and which documents the multifarious and ubiquitous appearances of the equilateral triangle throughout the natural and man-made worlds".
REFERENCES
- 'The Dissection of Rectangles into Squares' by R.L. Brooks, C.A.B. Smith, A.H. Stone, and W.T. Tutte in Duke Mathematical Journal, vol. 7, pages 312-40, 1940.
- 'The Dissection of Equilateral Triangles into Equilateral Triangles' by W.T.Tutte in Proceedings of the Cambridge Philosophical Society, Vol. 44, pages 464-82, 1948.
- 'On the Dissection of Rectangles into Right-Angled Isosceles Triangles.' in J Comb. Theory Ser. B Vol 80, 2, November 2000, pp. 277-319(43). by Skinner J.D.; Smith C.A.B.; Tutte W.T.
- Mathworld; Square Tiling
- Laczkovich, M. "Tilings of Polygons with Similar Triangles." Combinatorica 10, 281-306, 1990.
- Making Squares from Pythagorean Triangles Charles Jepsen, Roc Yang , The College Mathematics Journal, Vol. 29, No. 4 (Sep., 1998), pp. 284-288
- Ivars Peterson's mathTrek - Squaring Circles
- Pythagorean Theorem Extensions by Christina Lau, BA, The University of Texas at Austin August 2011
- Recreational Mathematics, Paul Yiu, Department of Mathematics, Florida Atlantic University (6.5 Dissecting a rectangle into Pythagorean triangles . . . . p214)
- 'Quadrillator', Tiling the smallest square with 5 Pythagorean triangles?
- Dr Ron Knott, Pythagoriean Jigsaws
- Brian J. McCartin, "Mysteries of the Equilateral Triangle"
- Andrzej Zak, A note on perfect dissections of an equilateral triangle Andrzej Zak, AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 44 (2009), Pages 87–93
- Aleš Drápal and Carlo Hämäläinen (July, 2010 ) :An enumeration of equilateral triangle dissections. (Discrete Applied Mathematics, Volume 158 Issue 14,)