Downloads

Bouwkamp Codes(zipped txt)
Catalogues of Squared Squares (Pdf)
- Catalogues of (low order <=30) Perfect Squared Squares by discoverer (Pdf's)
- Catalogues of Simple Perfect Squared Squares (Pdf's)
- Catalogues of Compound Perfect Squared Squares (Pdf's)
Catalogues of Right Isosceles Triangle Tilings
Software

Bouwkamp code

Squared rectangles and squared squares are often represented in a concise form known as Bouwkamp code (or bouwkampcode), named after C.J. Bouwkamp who invented this notation and popularised its use.

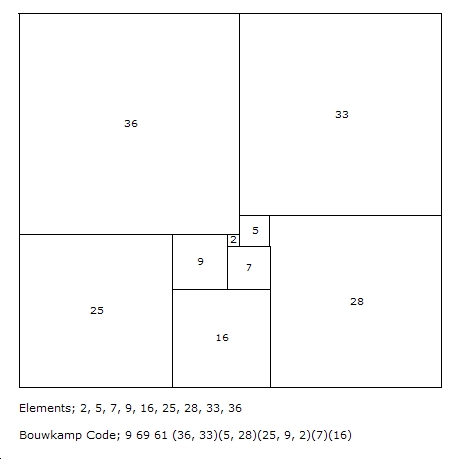
Bouwkamp code consists of a string of numbers giving firstly the number of squares in the dissection (called the Order), the width and height of the square dissection, where width >= height, and finally the sizes of the squares of the tiling, often called the elements, as integers e₁, e₂, e₃, ... e_n (with or without parentheses or commas), which are arranged from left to right and then top to bottom.

In the published literature parentheses and commas are used to group consecutive squares in a horizontal row and the groups are in order of decreasing height.

The Bouwkamp code parentheses are not required to reconstruct the tiling but they make it easier to sketch a tiling by hand and all published literature uses them. Bouwkamp code without parentheses and commas has been named tablecode and introduced by J.D. Skinner. It is simpler and shorter. The tablecode for the 69 x 61 Squared Rectangle figure above is 9 69 61 36 33 5 28 25 9 2 7 16. Tablecode, bouwkampcode and Bouwkamp code are used interchangeably in this site.

Rotations and reflections of a square tiling may create different Bouwkamp codes. Canonical Bouwkamp code is the unique code which is the highest Bouwkamp code, the one that is numerically largest (comparing elements going left to right) from the Bouwkamp codes of all possible rotated and reflected versions of that square tiling.

If squared rectangles and squared squares are put into canonical Bouwkamp code form, duplicates of existing tilings can easily be identified, new discoveries can be verified and complete catalogues for many low order tilings can be made in a compact text form, suitable for computer data processing, document production, browser viewing and computer graphics rendering.

For SPSR the canonical Bouwkamp code is also the one corresponding to the dissection where the largest corner element is in the top left corner and is listed first out of the elements. This is easy to check.

For SPSS only the first two elements need to be examined for highest Bouwkamp code, that is the largest square in the top left corner and largest square adjacent to it, which goes on its' right. These two elements are the first and the second listed elements in the canonical Bouwkamp code.

For Imperfect tilings (SISS, SISR) it may be necessary to examine all elements in the Bouwkamp code to determine the canonical highest Bouwkamp code.

For CPSS there is the additional complication of multiple possible orientations for subrectangles and tiled subsquares. Unfortunately many CPSS in the published literature are not recorded in any discernably consistent canonical Bouwkamp code representation.

On this website, for CPSS's we use the tiling with the highest Bouwkamp code in which each simple subrectangle is in 'standard form' so that, after first rotating the square one quarter turn clockwise if necessary, the subrectangle can be seen with its longer side horizontal and its largest corner element positioned in the upper left corner.

This applies to a simple subrectangle with a missing corner element as if that element were present but without the restriction on the amount by which the square may first be rotated (example: CPSS 27:849B).

If the compound square comprises two squares and two rectangles then only a tiling in which the two squares are in opposite corners is permitted (example: CPSS 28:1015B).

If two simple subrectangles overlap and share a corner element then possibly only one of them can be seen in 'standard form' (example: CPSS 39:1813A).

Jasper D. Skinner's Squared Squares Bouwkamp code (in tablecode form) from orders 21 to order 30

J.D. Skinner has supplied the following listing and tablecode for squared squares from orders 21 to order 30.

biglist.zip(41k) has a listing of the squared squares by order, size/id and type (SIMP/COMP) - the size/id is also used to refer to the corresponding Bouwkamp code in the 00table.zip file. Discoverers initials are included.

00table.zip(558k) contains the corresponding Bouwkamp codes (in tablecode form).

David Moews Bouwkamp codes

David Moews has an explanation and an example of the use of Bouwkamp code.

David Moews homepage has Bouwkamp codes of all simple perfect squared rectangles (SPSR) of orders from 9 to 16, and Bouwkamp codes of all perfect squared squares (PSS) of orders from 21 to 24 (and some of orders from 25 to 27.)

A.J.W. Duijvestijn's order 26 SPSS, 2x1 SPSR paper and Bouwkamp codes

The AMS has provided a free download of Duijvestijn's paper on Order 26 simple perfect squared squares (SPSS) and 2x1 simple perfect squared rectangles (SPSR). Copies have been supplied of the missing Bouwkamp codes TableI Order 26 SPSS and TableII Order 26 2x1 SPSR which originally accompanied the paper.

Display book catalogues of Perfect Squared Squares

Perfect simple and compound squared squares (PSS), Orders 21+, (20Mb Pdf).
Listings of squared square Bouwkamp codes provided to the website by J.D. Skinner, J. Haubrich and sourced from published articles and listings of Brooks, Smith, Stone & Tutte, A. J. Duijvestijn, C. J. Bouwkamp. and many others. Bouwkamp codes processed and edited for publication by S. Anderson and G. H. Morley. Converted to postscript and then to pdf (using Ghostview) by S. Anderson.

Perfect Squared Squares by discoverer (being updated)

Arthur Stone's squared square discovery (6k Pdf)
A.J.W. Duijvestijn's squared square discoveries (1.5Mb Pdf)
C. Müller's squared square discoveries (> order 30) (22k Pdf)
C. J. Bouwkamp's squared square discoveries (271k Pdf)
E. Lainez's squared square discoveries (7k Pdf)
Federico and Willcocks joint squared square discoveries (18k Pdf)
G. H. Morley's squared square discoveries (GHMcpss.Pdf and GHMspss.pdf)
Ian Gambini's squared squares. (He has also found 30,000+ pss in orders > 30) (8k Pdf)
J.C. Wilson's squared square discoveries (45k Pdf)
J.D. Skinner's squared square discoveries (17.8 Mb Pdf)
P.J. Federico's squared square discoveries (152k Pdf)
R.L. Brooks squared square discovery in order 39 (6 Pdf)
R.P. Sprague's squared square discovery (>30 but included as the first found) (8k Pdf)
S.E. Anderson's squared square discoveries (101k Pdf)
T.H. Willcocks' squared square discoveries (21k Pdf)
W.T. Tutte's squared square discoveries (11k Pdf)

Simple Perfect Squared Squares Orders 21+

(1) SPSS's Order 21, (5k Pdf)
(8) SPSS's Order 22, (14k Pdf)
(12) SPSS's Order 23, (19k Pdf)
(26) SPSS's Order 24, (39k Pdf)
(160) SPSS's Order 25, (220k Pdf)
(441) SPSS's Order 26, (619k Pdf)
(1152) SPSS's Order 27, (1.6M Pdf)
(2970) SPSS's Order 28, (4.4M Pdf) possibly incomplete
(3512) SPSS's Order 29, (5.3M Pdf) incomplete
(4490) SPSS's Order 30, (6.9M Pdf) incomplete
(376) SPSS's Order 31-75, (585k Pdf) incomplete

Compound Perfect Squared Squares Orders 24+

Compound perfect squared squares (CPSS), Orders 24 to 30, (786 Kb Pdf)
(1) CPSS's Order 24, (5k Pdf)
(2) CPSS's Order 25, (7k Pdf)
(15) CPSS's Order 26, (25k Pdf)incomplete.
(39) CPSS's Order 27, (58k Pdf) incomplete.
(92) CPSS's Order 28, (136k Pdf) incomplete.
(169) CPSS's Order 29, (238k Pdf) incomplete.
(224) CPSS's Order 30, (339k Pdf) incomplete.
(51) CPSS's Order 31 incomplete.
(36) CPSS's Order 32 incomplete.
(81) CPSS's Order 33 incomplete.
(43) CPSS's Order 34 incomplete.
(14) CPSS's Order 35 incomplete.
(4) CPSS's Order 36 incomplete.
(8) CPSS's Order 37 incomplete.
(7) CPSS's Order 38 incomplete.
(15) CPSS's Order 39 incomplete.
(2) CPSS's Order 40 incomplete.
(13) CPSS's Order 41 incomplete.
(6) CPSS's Order 42 incomplete.
(32) CPSS's Order 43 incomplete.
(22) CPSS's Order 44 incomplete.
(10) CPSS's Order 45 incomplete.
(18) CPSS's Order 46 incomplete.
(12) CPSS's Order 47 incomplete.
(0) CPSS's Order 48 incomplete.
(0) CPSS's Order 49 incomplete.
(0) CPSS's Order 50 incomplete.
(0) CPSS's Order 51 incomplete.
(2) CPSS's Order 52 incomplete.
(10) CPSS's Order 53 incomplete.
(24) CPSS's Order 54 incomplete.
(1) CPSS Order 55 incomplete.
(25) CPSS's Order 56 incomplete.
(26) CPSS's Order 57 incomplete.
(1) CPSS Order 58 incomplete.
(1) CPSS Order 86 incomplete.

Tiling Catalogues of Isosceles Right Triangled Squares

Primitive Perfects Catalogues

Non-ultraperfect Catalogues

Derivative Ultraperfects Catalogues

Simple Primitive Imperfects Catalogues

Software

David Moews simple perfect squared rectangles (SPSR) generator (GPL!)

David Moews homepage also has GPL'd software (written in C) to produce simple perfect squared rectangles (SPSR).

graph.c enumerates all simple perfect squared rectangles with order 20 or below (the order can easily be varied by editing the source). Each rectangle's order, size, and Bouwkamp code is printed, one rectangle to a line. Also, some statistics on graphs used to generate the rectangles are printed.

From the readme;

graph.c

This program enumerates simple perfect squared rectangles. Here, a _squared_rectangle_ is a rectangle dissected into squares. It is _perfect_ if no two of the squares are the same size, and _imperfect_ otherwise. It is _simple_ if it contains no smaller squared rectangle, other than its component squares; if it is not simple, it is _compound_. The number of squares a squared rectangle is divided into is called its _order_.

A squared rectangle can be described by its _Bouwkamp_code_. This code is obtained by looking at a list of the horizontal segments found in the squared rectangle, ordered from top to bottom and starting with the top edge, and making, for each segment, a parenthesized list of the side-lengths of the squares immediately below the segment, going from left to right.

graph.c enumerates all simple perfect squared rectangles with order 20 or below. Each rectangle's order, size, and Bouwkamp code is printed, one rectangle to a line. Also, some statistics on graphs used to generate the rectangles are printed; see below. Some rectangles will be printed more than once.

Method

------

According to the seminal paper of Brooks, Smith, Stone, and Tutte (Duke Math. J., 7 (1940), pp. 312--340, (5.23)), any simple perfect rectangle can be derived from a 3-connected planar graph in the following way: some edge of the graph is deleted; the remaining graph is then viewed as an electrical network by giving each remaining edge a resistance of one ohm, and applying a unit potential across the pair of vertices the deleted edge was attached to. Each edge can then be associated with a square whose size is proportional to the current flowing through the edge; Kirchoff's laws ensure that these squares can be assembled into a rectangle.

The program enumerates the 3-connected planar graphs by successively splitting vertices and faces as described in Dillencourt (J. Comb. Theory B, 66 (1), Jan. 1996, pp. 87--122, Thms. 4.1, 4.2), and a unique representative from each isomorphism class is chosen using the algorithm described in Hopcroft and Tarjan (J. Computer & System Sciences 7 (1973), pp. 323--331). For each given number of vertices, edges, and faces, and automorphism group size, the program prints the number of self-dual and non-self-dual graphs with these characteristics.

David Moews, 13-XI-2004 dmoews AT xraysgi.ims.uconn.edu

Stuart Anderson's 'ssh.exe' (squared square hunter - finds SPSS, SISS, SPSR and SISR)

I have produced a (windows command-line) program ssh (squared square hunter) which searches for simple perfect or simple imperfect squared squares (SPSS or SISS) in the c-nets produced by Brinkmann and McKay's plantri program. Ssh.exe can also be used to produce simple perfect or simple imperfect squared rectangles (SPSR or SISR). If you type the executable name you will see a screen like this;

ssh - Squared Square Hunter by Stuart Anderson,
Squared Squares are dissections of squares into smaller squares, all integer sizes and preferably all different sizes.
Squared Square Hunter (ssh) generates squared squares and squared rectangles from plantri generated 3-connected planar maps.
Plantri is by Gunnar Brinkmann and Brendan McKay and is available from http://cs.anu.edu.au/~bdm/plantri/ .
ssh has many options and combinations
Syntax is: ssh [-scpirSthd] filename (filename is a plantri binary file).
[-scpirSht] are the optional arguments.
- s (lower case) for simples
- c for compounds - not implemented
- p for perfects
- i for imperfects
- r for rectangles
- S (upper case) for squares
- h for bouwkampcode in html output.
- t for tablecode output, i.e. w h followed by elements in bouwkampcode order (no parentheses).
- d for screen display/file dump, better on for squares rather than rectangles (slows things down)
If no arguments are given, default options used are -spiSt i.e. simple perfect and imperfect squares output in table format.

The output of ssh is saved as bouwkampcode and html code bouwkampcode files are named with prefix 'o', then a number for the order, and pss or iss for perfect simple or imperfect simple squares. The order is the number of squares in the square/rectangle or one less than the corresponding number of edges in the graph.

Points to Note;

As explained in the above quote, you need a plantri file for the program to work on.
Download and compile the plantri source from Brendan McKay's website.
For windows users who want a compiled program, download this plantri.exe binary and put it in your PATH
Here is an example, we will be generating simple perfect squared rectangles with 16 squares;
Firstly you need to generate all c-nets with 17 edges (number of edges is one more than the number of squares).
Look at the table at Numericana to see which classes of graphs we need to generate.
The first magenta diagonal has the numbers of polyhedral graphs (c-nets) with 17 edges ie 38+633+633+38=1342
We dont need all 4 of these graph classes (the first 38 are dual to the last 38 and produce the same squared rectangles, rotated 90%, same for the two 633's)
Get a commandline window up and set the current directory to the folder with plantri and ssh in it (if these are not in the PATH already), then generate the required c-net files using plantri;
- >plantri -pde17 10 e17v10.bin
- >plantri -pde17 11 e17v11.bin
The previous two lines generate c-nets with 17 edges and 10 and 11 vertices,i.e;
>plantri -pde17 10 generates all the duals of polyhedron graphs with 17 edges and 10 vertices
>plantri -pde17 11 generates all the duals of polyhedron graphs with 17 edges and 11 vertices
e17v10.bin and e17v11.bin are the names we give the output files (we could use any names)
Now generate the squared rectangle bouwkampcode using ssh.exe;
- >ssh -sprh e17v10.bin
- End of File e17v10.bin
- 633 graph(s) processed in 64.625 sec from plantri file e17v10.bin
- 8633 simple perfect squared rectangles saved to file o16spsr.html
- >ssh -sprh e17v11.bin
- End of File e17v11.bin
- 38 graph(s) processed in 4.282 sec from plantri file e17v11.bin
- 383 simple perfect squared rectangles saved to file o16spsr.html
The end result is file o16spsr.html with 8633+383=9016 simple perfect squared rectangles.
- The file should be viewed in a text editor (not a browser - I generated it this way to assist in building my website - the html is a form select menu and wont render without javascript and a frameset).
- A good text editor can be used to strip away the html tags and you are left with the bouwkampcode. If you want bouwkampcode in tablecode form, use ssh. with the t switch not h switch for example, >ssh -sprt e17v11.bin.
Be careful when generating squared rectangles in orders 20+, you can generate hundreds of Megabytes, even Gigabytes of bouwkampcode quite easily.
If squared squares are what you are interested in, remember all squared squares up to order 28 are known and already searched for. You need to do order 29 and up, even then many are known.
If you think you have a new discovery, check the website catalog first, if it is not listed, contact me at stuart(the AT symbol)squaring.net and I will credit you with the discovery.
The plantri files are so large in the higher orders you will need to split them up using the res/mod option see the plantri-guide for an explanation.
Squared squares, unlike squared rectangles are rare and hard to find. You may only find one or two or perhaps none over a 24 hour computer run.
Use >ssh -spihSd plantrifile for squared squares (or >ssh -spitSd plantrifile, if you prefer tablecode).
This will produce imperfect squares as well as perfects (imperfects are quite rare too and you might as well collect them along the way - it wont slow the search down) I also use the d switch so you can see any discoveries as they occur.
If you are interested in finding Compound squared squares my software is not designed for that, it is better to generate them by searching for squared rectangles and fitting them together and by using transform techniques (see the book Squared Squares: Who's Who & What's What, by Jasper Dale Skinner II - available from the author)

Armin Singer's squaredance

Armin Singer has produced squaredance to display simple perfect squared squares as a slideshow. Designed for Xwindows (linux, unix). On linux, "tar xzf squaredance-0.5.tgz" will unpack the package and put its files into a subdirectory named squaredance-0.5. Invoking "make" in this directory should produce the squaredance executable.

The squaredance package will show you simple perfect squared squares using XVideo. Most parts of it are taken form Open Source (xorg,tvtime). Only a few things have been added by asi AT equicon.de. Some of this parts are "quick and dirty hack", sorry for this. Especially, the program relies on datafiles being correct. Enjoy it, but do not fight against minor strange effects (varying line width, interfering colors). There is no fancy GUI but just the things needed to enjoy the show.

By default, the squaredance executable uses spss.dat and a delay of 1000ms between frames. Please refer to main.cpp for supported options and/or just try; ./squaredance --help

The package contains the following source files:
- bars.[ch]pp ............. some code dealing with horizontal "bars", used to convert Bouwkamp codes to drawable information
- findflips.c ............. short C program used to create flips.dat (see below) - not needed to build the squaredance executable
- main.cpp ................ main squaredance module - look at this first
- makefile ................ the package makefile to be used by make(1)
- myxev.c ................. a modified xev.c from the X sources
- squaredance.[ch]pp ...... the squaredance core machinery using xvideoshow.*
- xvideoshow.[ch]pp ....... XVideo code taken from the tvtime source RPM
- Some datafiles containing lines with Bouwkamp codes have been provided:
- crosses.dat ............. some simple perfect squared squares with a "cross"
- flips.dat ............... some pairs of SPSS having the same elements
- nice.dat ................ "nice" SPSS samples (no tiny elements)
- spss.dat ................ almost all SPSS from www.squaring.net

Richard Parris windisc program

Windisc displays squared rectangles and their associated c-nets (WinXP)

See Richard Parris 'peanut software homepage' for a range of maths programs and his windisc page for a copy of that software.

To use windisc to view squared rectangles and c-nets, start the program, select Windows -> graphs, then select File -> New -> Squared Rectangle. Some of the viewing parameters can be edited under View -> Squared Rectangles.

Richard Parris windisc program