Squared Squares - Introductory links |
 |
Mathworld Perfect Square Dissections |
 |
Ed Pegg's Math Games - Square Packing |
R.L. Brooks, C. A. B. Smith, A. H. Stone and W. T. Tutte |
 |
The Dissection of Rectangles into Squares. 1940 |
|
Determinants and current flows in electric networks 1990 (subscription) |
| The Trinity Mathematical Society |
Skinner J.D.; Smith C.A.B.; Tutte W.T. |
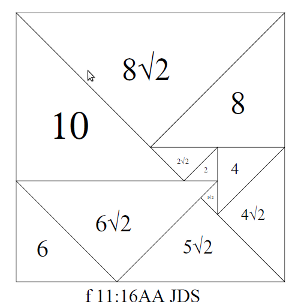 |
On the Dissection of Rectangles into Right-Angled Isosceles Triangles. |
CAB Smith |

C.A.B. Smith (CABS)
|
The Story of Blanche Descartes |
| In Memoriam, Cedric A B Smith [link to be updated] |
| Times Online CAB SMITH Obituary [link to be updated] |
Arthur Stone |
 |
An Interview with Arthur Stone, by W. W. Comfort |
William T Tutte |

BBC: Code Breakers Bletchley Parks lost Heroes (Tutte and Flowers)
|
| Biographical memoir of Bill Tutte (by Dan Younger for the Royal Society) |
| A review of W T Tutte's 'Graph Theory as I have known it' (PDF) |
| A Toast to Matroids by W. T. Tutte |
| 60 Years in the Nets by W. T. Tutte (audio Realplayer 7) |
| W T Tutte CRM-Fields Institute Prize |
| Tutte honored by cryptographic centre, June 17, 1998 |
| Bill Tutte's role in the programming of the worlds first digital computer - kept Top Secret until recently. It is said Bill Tutte and Tommy Flowers shortened WWII by 2 years |
Code-Breakers: Bletchley Park's Lost Heroes - BBC Two.
The story of Bill Tutte and Tommy Flowers. The two mystery men who uncovered Hitler's secret code and helped win WW2, then disappeared from history. |
 |
During his time at Bletchley Park, Captain Roberts came into contact with several brilliant men. He says, in the great successes of Bletchley Park,
three men played key roles. Alan Turing (who possibly saved Britain by breaking naval Enigma in 1941), Bill Tutte (who broke the Tunny
cipher-system, helping to shorten the war, as Gen. Eisenhower said: Bletchley decrypts shorten the war by at least two years) and Tommy Flowers
(who designed and built Colossus, the first electronic computer ever, the Founding Father of todays computer world).
17SEP2009: Captain Jerry Roberts visits the Google London office to speak about his time as a code breaker at Bletchley Park during World War 2. This
talk took place as part of the Speakers@Google series, on the 24th August 2009. (1h7m45s) |
| 1FEB2010: Unsung heroes of IT: The story of Bill Tutte and Tommy Flowers (7m9s) |
| Unsung Heroes: The story of Bill Tutte (14m41s) |

Colossus reconstructed
|
27MAY2011: Code-cracking machine returned to life (3m12s) The first Tunny machines were built following the work in 1942 of
mathematician Bill Tutte. |
| 2FEB2010: Bletchley's code-cracking Colossus |
| A Brief History of Computing (including Colossus). It mentions DEUCE which I
was shown in 1957 (at English Electric, Whetstone near Leicester) by a Mr. Lam from Vietnam who worked there. It also mentions Maurice Wilkes
(1913-2010) who built EDSAC in 1949: I attended some of his lectures in Cambridge. (Geoffrey Morley) |
W. T. Tutte
|
The Guardian William Tutte |
| William T Tutte - Mathematician |
 |
CJ Bouwkamp |
| CJ Bouwkamp en de Squared Squares (Dutch); J Haubrich (PDF) |
AJW Duijvestijn |
| ELECTRONIC COMPUTATION OF SQUARED RECTANGLES, AJW Duijvestijn |
| In memoriam Arie Duijvestijn (Dutch) |
| Recollections of Duijvestijn (Dutch) |
| A. J. W. Duijvestijn publications |
| Duijvestijn SPSS and 2x1 Squared Rects order 26 (PDF) |
 |
JD Skinner II |
|
Uniquely squared squares of a common reduced side and order 1992 |
|
Ian Gambini |
|
Ian Gambini's 2001 thesis Carres (French) (PDF) |
 |
T.H. Willcocks |
|
TH Willcocks the chess composer and squared square pioneer. |
|
Graph Theory, Enumeration, Generation and Representation of Planar Graphs |
|
|
Mathworld: Polyhedral Graph
|
| Blanche Descartes Review of Bondy and Murty's 'Graph Theory with Applications' |
| W.T.TUTTE, A New Branch of Enumerative Graph Theory, 1962 |
| Enumeration of Polyhedra - Numericana |
| Duijvestijn; The number of polyhedral (3-Connected Planar) Graphs |
| Duijvestijn; Identification of Graphs, Two graphs have the same identification number if and only if they are isomorphic. |
| CaGe -- Chemical & abstract Graph environment - software with a graphical user interface to produce and view graphs (includes plantri generators) |
| plantri - planar graph software (produces many kinds of planar graph, including polyhedral graphs) by Brendan McKay and Gunnar Brinkmann |
| Plantri-full. This paper describes plantri’s principles of operation, the basis for its efficiency,
and the recursive algorithms behind many of its capabilities. |
| convex polytopes - representations and 3D embeddings |
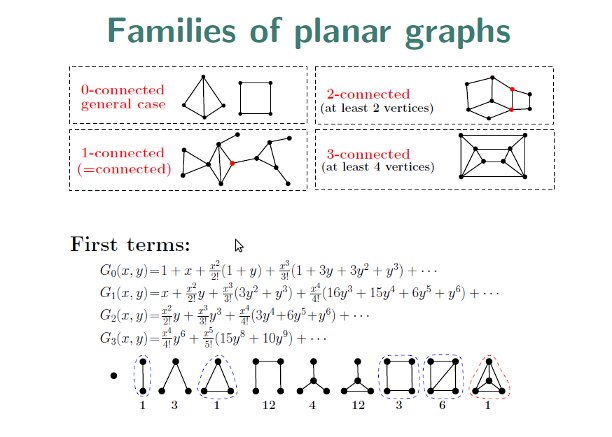 |
Bodirsy, Gropl, Johannsen and Kang; c-net enumeration |
| ASYMPTOTIC ENUMERATION AND LIMIT LAWS OF PLANAR GRAPHS OMER GIM´ENEZ AND MARC NOY |
| Bodirsky; 10 Steps to Counting Unlabeled Planar Graphs: 20 Years Later |
| Fusy; Decomposition and enumeration of planar graphs |
| Peter Eades (Sydney) How to Draw a Graph, Revisited |
| A106651 c(n) = number of c-nets on n vertices. |
| A000109 Number of simplicial polyhedra with n nodes; simple planar graphs with 3n-6 edges; maximal simple planar graphs; 3-connected planar triangulations; 3-connected triangulations of the sphere; 3-connected cubic planar graphs. |
| A000944 Number of polyhedra (or 3-connected simple planar graphs) with n nodes. |
| A049337 Triangle read by rows: T(n,k) = number of 3-connected planar graphs (or polyhedra) with n >= 1 nodes and 0<=k<=C(n,2) edges. |
Squared Rectangles, and Variations on Square and Rectangle tiling |
|
Bjarne Pagh Byrnak's Squared rectangle calculator. |
 |
Robert Haramoto - Simple Perfect Squared Rectangles |
| Prolog III, Alain Colmerauer - Squaring Rectangles p 25-31(PDF) |
| Squaring Rectangles and VLSI layouts - Prof Wai-Kai Chen |
| Tilings; Benjamin Blander & Darren Lo (PDF) |
| Global Constraint Catalog - Squared squares |
| Beentjes squared rectangle method(PDF) |
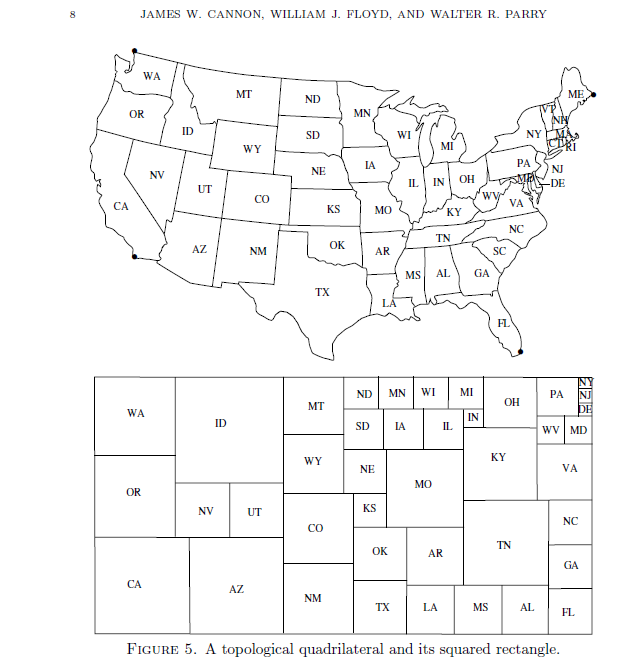
| Cannon, Floyd and Parry's paper - Squared rectangles & Riemann mappings(PDF) |
| Cannon, Floyd and Parry's software for squared rectangles and circle packing |
| Shastry - Squared rectangle algorithms(PS) |
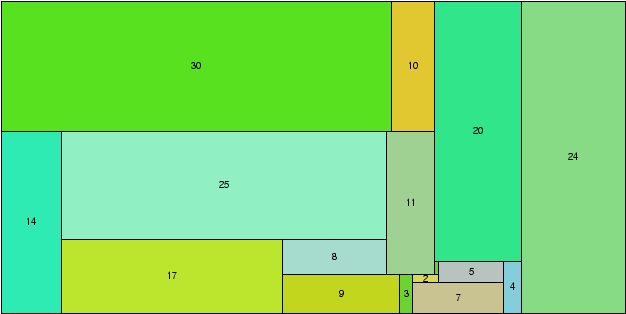 Giovanni Resta's Perfect Rectangles Giovanni Resta's Perfect Rectangles
|
The dissection of rectangles, cylinders, tori and Mobius strips into squares ; S J Chapman (subscription only) |
| Eric Friedman's Math Magic - has many variations on the square packing theme |
| Squared rectangles: A space-efficient layout for ranked graphics |
| Eppstein's Geometry Junkyard Dissections |
| Yoshiro Mimura's Page of Square Identities |
| Robert Wainwright's Partridge Puzzle Page |
| The 7070 Square Puzzle |
| Patterns with right angled Isosceles Triangles |
| triangle dissections (including integer dissections) |
| Proof by David Radcliffe that there are no perfect triangled triangles |
| Giovanni Resta's Perfect Rectangles |
 |
Pascal Huybers' Puzzles with squares |
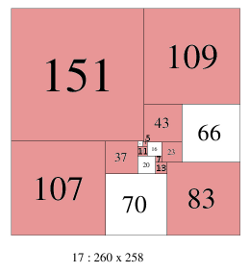 |
Problem 48.? Simple perfect prime squared rectangles |
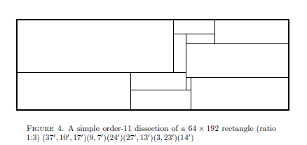 |
Dissections of p:q rectangles; Jepsen (PDF) |
 |
Artwork I recently (2022) made for the 50th birthday of my friend, artist Tamás Veszi (USA). |
 |
"For the 50th Birthday of my Friend, Hungarian-American Artist, Tamás Vészi, 25x25cm, mixed technique by hand, 2022, photo © Grego, 2022 and photo of Tamás Vészi with his present by Grego)"
Grego Foldvari |
 |
John Shier's work on fractal space-filling with squares, (In fact with any shape). John's interesting discovery is that one can fill all space by placing ever-smaller shapes at random without overlap (the areas of the shapes must follow a prescribed sequence). In the limit where one places an infinite number of shapes, they completely fill the space in fractal fashion. The evidence is that any shape will work. It may seem surprising, but all of these varied images are examples of the same algorithm. The rules only apply to the shapes -- the color scheme can be chosen arbitrarily.
Links to further work and examples from John Shier are here. Related work by Paul Bourke is here
|
The Squaring Game - a free online tiling game by Prelude Games
|
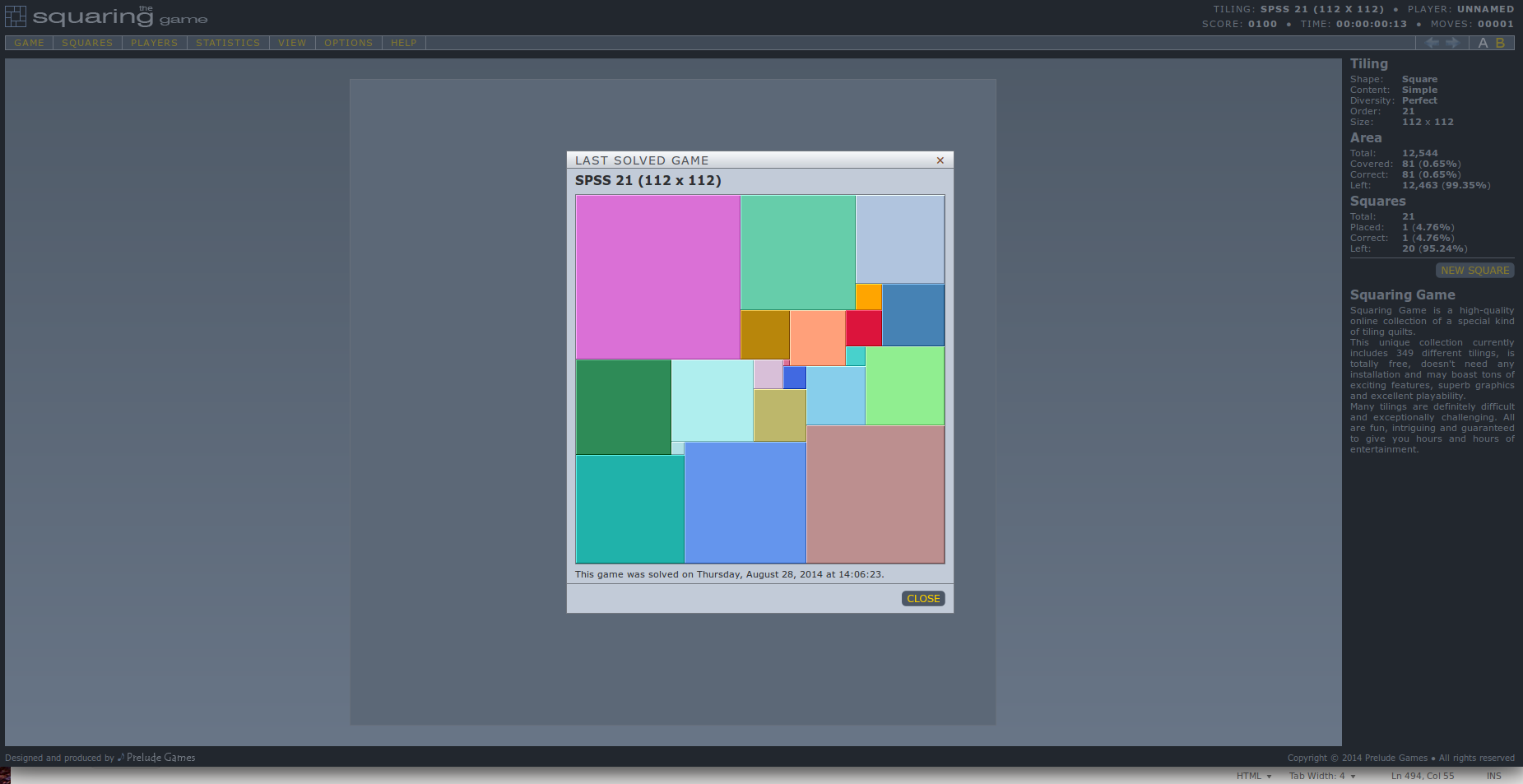 |
Squaring Game addresses a special kind of tiling puzzles or, more appropriately, tiling quilts, and is based on a well-known mathematical problem called "square packing" or, seen from a different perspective, "square (or rectangle) dissection".
When a game starts, a square (or a rectangle) is divided into smaller squares of various sizes, each with its own color. Rearranging these squares into the original square (or rectangle) is the purpose of the game. Please note that each tiling has one, and only one, solution.
Since squares have even edges and do not stick together, each of them has to be positioned in its exact place on stage A in order to solve the game. Although squares are automatically snapped along a preset grid, their precise rearrangement is your own task. |
Squared Square Arty & Crafty
|
 |
The Mathematical Art Galleries website – the online home of the mathematical art exhibits from the annual Bridges Conference and Joint Mathematics Meetings (JMM), features the work of Horst Schaefer who has exhibited Mondrian style acrylic paintings of a SPSS (Duijvestijn's order 21 112 square), a CPSS (Willcocks's order 24 175 square) and a SISS (Bouwkamp's order 13 23 square) |
 |
David Spiegelhalter's stained glass of Duijvestijn's order 21 112 square on a snowy day |
 |
MATH with my KIDS; Latin Squares, Squared Squares, and Legoed Squares |
 |
Artist Eric Harshbarger's Perfect Square Dissection of the 21 Duijvestijn square in LEGO |
 |
Carsten Nicolai's sculpture - includes the Duijvestijn 112 squared square in glass sheets (2004) |
 |
Armin Singer's 3D printed Simple Perfect Squared Square (SPSS) frame models |
 |
Stijn's PostScript fragment |
 |
Rob's Puzzle Page |
 |
Square Deal - Squared Squares in Fabric |
 |
Crafting by Concepts: Fiber Arts and Mathematics - Google Books Result -Chapter 7 Perfectly Simple Squaring the Rectangle |
 |
Bob Mackay has build a wooden cabinet based on Duijvestijn's 21 112x112 squared square. See also with doors and drawers open and the front view (closed up) |
 |
Lorenz Milla's bookshelf based on the Duijvestijn 112 squared square.
Lorenz gave some information on the materials and construction. "It's glued spruce/fir wood, 18mm thick
The wood was sawed into fitting pieces, then joined with standard screws after drilling holes. Was a bit tricky to decide which screw to fix first.
It took two hours of planning, one hour of shopping, and four hours of screwing (by hand). Next time I'll use the electric screwdriver".
|
Electrical Network Theory |
|
Electricity is NOT a form of energy!!! |