Squared Möbius Strips
The Möbius strip or Möbius band (UK /ˈmɜrbiəs/ or US /ˈmoʊbiəs/; German: [ˈmøːbi̯ʊs]), also Mobius or Moebius, is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.
A model can easily be created by taking a paper strip and giving it a half-twist, and then joining the ends of the strip together to form a loop. In Euclidean space there are two types of Möbius strips depending on the direction of the half-twist: clockwise and counterclockwise. That is to say, it is a chiral object with "handedness" (right-handed or left-handed).
The Möbius band (equally known as the Möbius strip) is not a surface of only one geometry (i.e., of only one exact size and shape), such as the half-twisted paper strip depicted in the illustration to the right. Rather, mathematicians refer to the (closed) Möbius band as any surface that is homeomorphic to this strip. Its boundary is a simple closed curve, i.e., homeomorphic to a circle. This allows for a very wide variety of geometric versions of the Möbius band as surfaces each having a definite size and shape. For example, any closed rectangle with length L and width W can be glued to itself (by identifying one edge with the opposite edge after a reversal of orientation) to make a Möbius band. Some of these can be smoothly modeled in 3-dimensional space, and others cannot
Topologically, the Möbius strip can be defined as the square [0,1] × [0,1] with its top and bottom sides identified by the relation (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1, as in the diagram on the right.
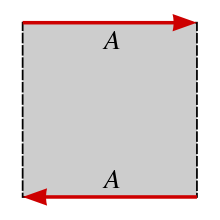
Gluing opposite edges of
a square to create a Möbius strip.
The Möbius strip is a two-dimensional compact manifold (i.e. a surface) with boundary. It is a standard example of a surface which is not orientable. In fact, the Möbius strip is the epitome of the topological phenomenon of nonorientability. This is because 1) two-dimensional shapes (surfaces) are the lowest-dimensional shapes for which nonorientability is possible, and 2) the Möbius strip is the only surface that is topologically a subspace of every non-orientable surface. As a result, any surface is non-orientable if and only if it contains a Möbius band as a subspace.