Simple Perfects with Crosses

Some the earliest known perfect squares featured crosses in their construction. For example, Sprague's square of order 55, side 4205.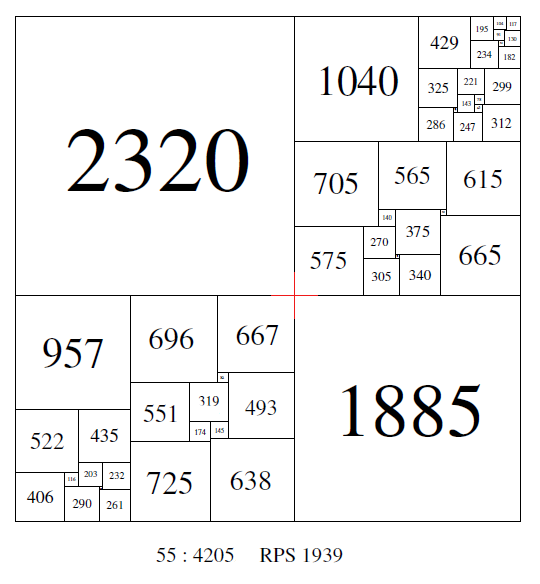

A compound perfect squared square found by Roland Brooks, using the rotor-stator symmetry method, has 2 crosses;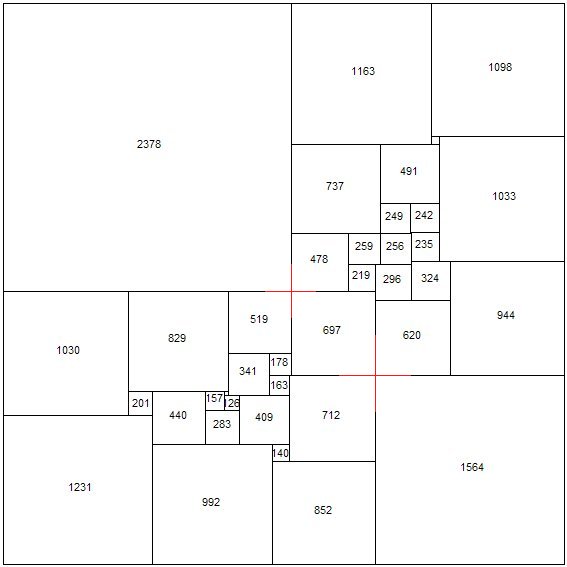

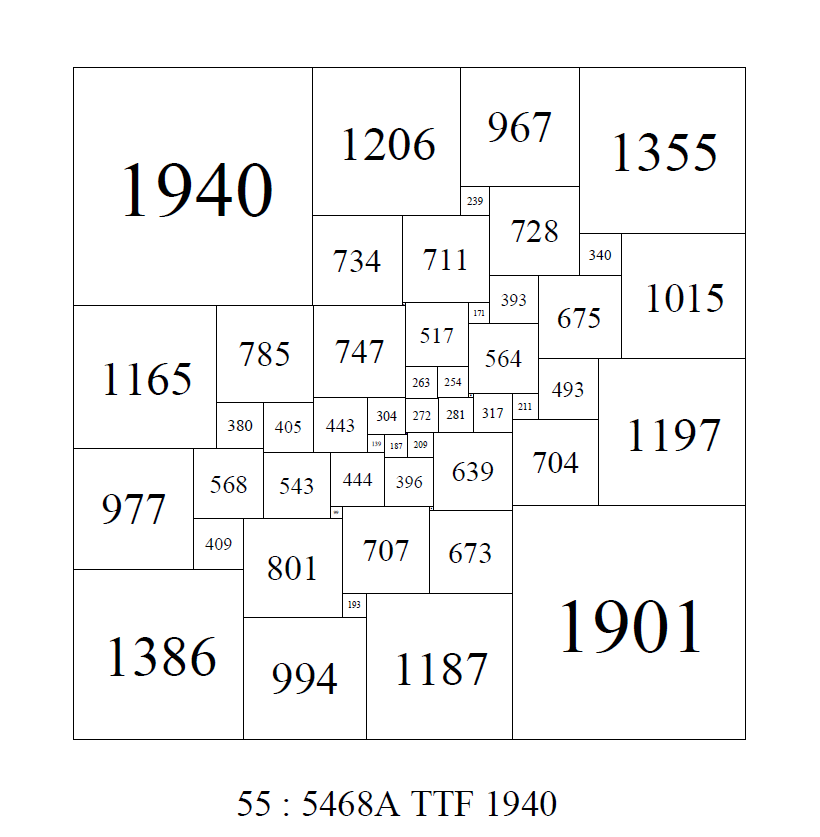
A compound perfect squared square found by Arthur Stone, using 2 order 13 simple perfect squared rectangles,

and 2 additional squares, has a cross. This is the R1, R2 Moron construction and is a crossed construction;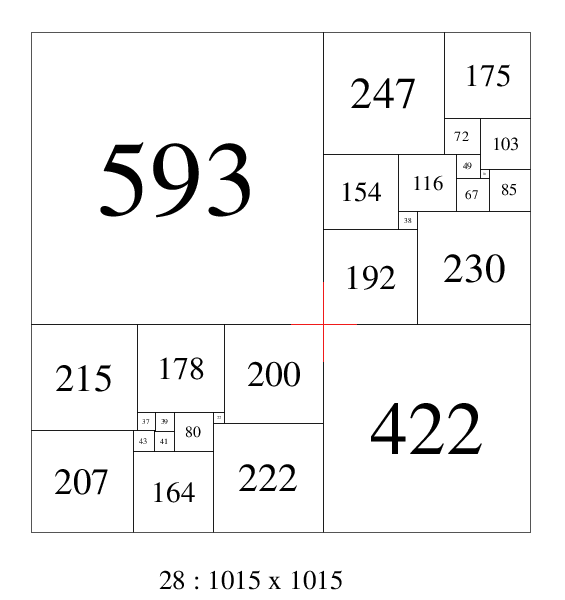

There are versions(isomers) of this CPSS without the cross;

In Brooks, Smith, Stone, Tuttes 1940 paper "The Dissection of Rectangles into Squares" they referred to an order 55 SPSS created using advanced rotor stator techniques.  The square had no cross and this was regarded as an achievement.  The cross being regarded as a 'blemish', indicative of the construction, which should be eliminated  where possible, although it was quickly realised that Perfect Squares with crosses were quite a rare phenomena.

Duijvestijn recorded the bouwkampcode and the orders in which crosses first appeared.  In order 26 he found the first SPSS with a cross of lowest order[1]. He also found the lowest order CPSS with a cross in order 26. The lowest order SPSR and SISR with a cross are in order 17 and and the lowest order SISS with a cross is in order 18.   I have extended the counts a little further to order 20 for squared rectangles and order 28 for squared squares.

THE NUMBERS OF CROSSED SQUARED RECTANGLES AND SQUARED SQUARES

Order	SPSR	SISR	SPSS	CPSS	SISS	CPSR
9	-	-	-	-	-	-
10	-	-	-	-	-	-
11	-	-	-	-	-	-
12	-	-	-	-	-
13	-	-	-	-	-
14	-	-	-	-	-
15	-	-	-	-	-
16	-	-	-	-	-
17	2	5	-	-	-
18	2	8	-	-	2
19	7	36	-	-	-
20	29	72	-	-	10
21	166		-	-	4
22			-	-	58
23			-	-	57
24			-	-	366
25			-	-	351
26			1	1	1858
27			3		1998
28			10

[1] SIMPLE PERFECT SQUARED SQUARES AND 2 x 1 SQUARED RECTANGLES OF ORDER 26,

 A.J.W. DUIJVESTIJN.

MATHEMATICS OF COMPUTATION, Volume 65, Number 215 July 1996, Pages 1359-1364