Simple Perfect Squared Rectangles with Isomers
Isomers are squared tilings with the same elements arranged differently. They have an important historical role to play in the research conducted by Brooks, Smith, Tutte and Stone.
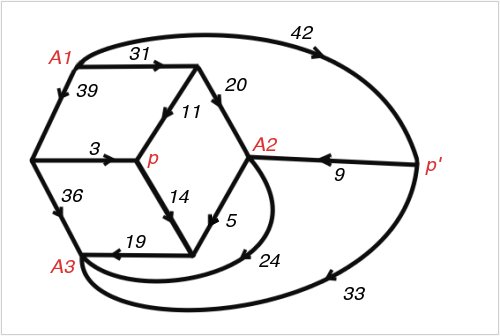
Figure 74; 112 x 75A Smith Diagram
Tutte wrote, "It was a pleasing recreation to work out perfect rectangles corresponding to networks with a high degree of symmetry. We considered, for example, the network defined by a cube, with corners for terminals and edges for wires. This failed to give any perfect rectangles. However, when complicated by a diagonal wire across one face, and flattened into a plane, it gave the Smith diagram of Figure 74 and the corresponding squared rectangle of Figure 75. This rectangle is especially interesting because its reduced elements are unusually small for the thirteenth order. The common factor of the elements is six. Brooks was so pleased with this rectangle that he made a jigsaw puzzle of it, each of the pieces being one of the component squares."
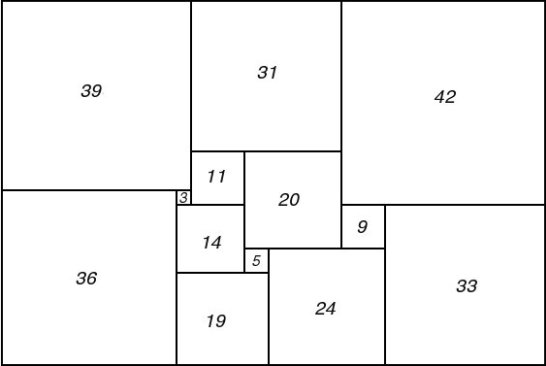
Figure 75; 112 x 75A Squared Rectangle
"It was at this stage that Brooks's mother made the key discovery of the whole research. She tackled Brooks's puzzle and eventually succeeded in putting the pieces together to form a rectangle. But it was not the squared rectangle which Brooks had cut up!
Brooks returned to Cambridge to report the existence of two different perfect rectangles with the same reduced sides and the same reduced elements."
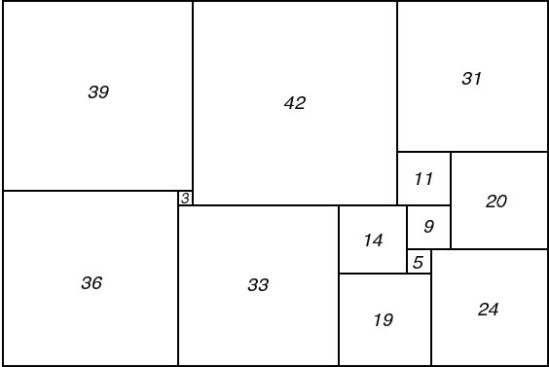
Figure 75; 112 x 75B Squared Rectangle
This led the researchers to examine the electrical networks of the two rectangles, they found they were related by symmetry. Further exploration of symmetry led to networks which could produce rectangles of the same size with all elements different (or with a single corner element the same), these can be assembled, with 2 other squares, to form a compound perfect squared square.
Duijvestijn cataloged isomers. In order 25 SPSS he found 3 pairs of isomers [1].
Isomers can be classified by the number in each class;
- Two – pairs
- Three – triples
- Four – quadruples
- Five – quintuples
- Six – sextuples
- Seven – septuples
- Eight – octuples
- Nine – nonuples
- Ten – decaples
- Eleven – undecaples
- Twelve – duodecaples
- Thirteen – tridecaples
- Fourteen – quadecaples
- Fifteen – quindecaples
- Sixteen – sexdecaples
- Seventeen – sepdecaples
- Eighteen – octdecaples
- Nineteen – nondecaples
The following counts are a final tally of sorted adjacent isomers by
order
CPSS always exist as isomers, the breakdown into equivalence classes is not shown (yet). It is also possible for simples and compounds of the same dimensions and order to form isomers. CPSRs have not been produced except at low orders.